题目内容
如图所示，直角△ABC中，∠BCA＝
，作AB边上高CF0，此时图中有三个直角三角形：△ABC、△BCF0、△ACF0；又作△ACF0边上AC上的高F0F1，此时图中有5个直角三角形；除前面3个外，增加了2个直角三角形△AF0F1，△F0F1C；按照同样办法作高F1F2，F2F3…当作到Fn－1Fn时，图中一共有多少个不同的直角三角形呢？
答案：
解析：
提示：
解析：
|
共有(2n＋3)个不同的直角三角形． |
提示：
|
练习册系列答案
阅读快车系列答案
相关题目
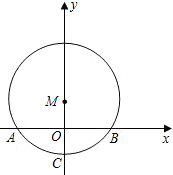如图，在⊙M中，
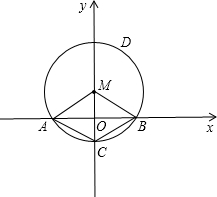如图，已知⊙M的半径为2cm，圆心角∠AMB=120°，并建立如图所示的直角坐标系．
如图所示，直角三角形ABC中，∠C=90°，AB=5cm，BC=3cm，则以AC为直径的半圆（阴影部分）的面积为（ ）
将如图所示的直角梯形绕直角边AB旋转一周，所得几何体的主视图是（ ）
如图所示，直角三角形ABC中，∠C=90°，AC=3，AB=5，BC=4，求点C到AB的距离．