题目内容
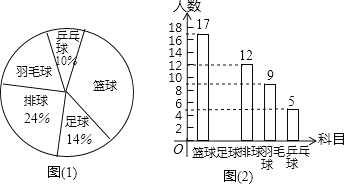
【题目】如图1,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
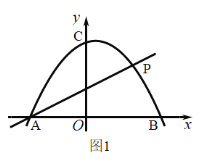
(1)求抛物线的函数关系式;
(2)点![]() 是抛物线第象限上一点,设点
是抛物线第象限上一点,设点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,如果点
,如果点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 落在
落在![]() 轴下方(含
轴下方(含![]() 轴),求
轴),求![]() 的取值范围;
的取值范围;
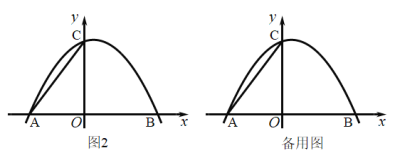
(3)如图2,连接![]() 将
将![]() 绕平面内某点
绕平面内某点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() 点
点![]() 的对应点分别是点
的对应点分别是点![]() 、若
、若![]() 的两个项点恰好落在抛物线上,请直接写出点
的两个项点恰好落在抛物线上,请直接写出点![]() 的坐标 .
的坐标 .
【答案】(1)![]() ;(2)
;(2)![]() 的取值范围为
的取值范围为![]() ; (3)点
; (3)点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)直接利用待定系数法即可求解;
(2)首先根据二次函数的解析式求出B,C的坐标,然后设点![]() 关于直线
关于直线![]() 对称的点恰好在
对称的点恰好在![]() 轴上时,对称点为
轴上时,对称点为![]() ,根据轴对称的性质和勾股定理求出点E的坐标,进而求出直线AP的解析式,然后将直线AP的解析式与二次函数的解析式联立,求出P点的横坐标,然后数形结合即可得出答案;
,根据轴对称的性质和勾股定理求出点E的坐标,进而求出直线AP的解析式,然后将直线AP的解析式与二次函数的解析式联立,求出P点的横坐标,然后数形结合即可得出答案;
(3)分两种情况:当![]() 在二次函数图像上时和当
在二次函数图像上时和当![]() 在二次函数图像上时,设点
在二次函数图像上时,设点![]() 的坐标为
的坐标为![]() 将点的坐标代入二次函数中,通过联立求方程组的解即可得出答案.
将点的坐标代入二次函数中,通过联立求方程组的解即可得出答案.
![]() 二次函数
二次函数![]() 的图象过点
的图象过点![]()
![]()
![]()
即![]() ;
;
![]() 令
令![]() ,则
,则![]()
解得![]() ,
,
![]() ,
,
令![]() ,则
,则![]()
![]() ,
,
则![]()
设点![]() 关于直线
关于直线![]() 对称的点恰好在
对称的点恰好在![]() 轴上时,对称点为
轴上时,对称点为![]() ,
,
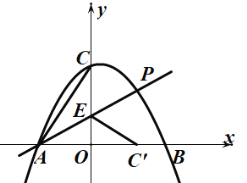
![]() ,
,
![]()
设![]() 长为
长为![]()
则![]()
在![]() 中,
中,![]() ,
,
即![]()
解得![]()
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的函数表达式为
的函数表达式为![]()
所以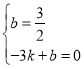 解得
解得![]()
即![]() .
.
设直线![]() 与二次函数的图像交点的横坐标为
与二次函数的图像交点的横坐标为![]() ,
,
则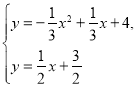
解得![]() ,
,
![]() 点
点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 落在
落在![]() 轴下方(含
轴下方(含![]() 轴)时,
轴)时,
![]() 的取值范围为
的取值范围为![]() ;
;
![]() 设点
设点![]() 的坐标为
的坐标为![]()
当![]() 在二次函数图像上时,
在二次函数图像上时,
则点![]() 的坐标为
的坐标为![]() 、点
、点![]() 的坐标为
的坐标为![]()
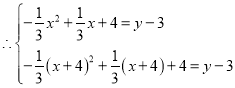
解得 ,
,
即点![]() 的坐标为
的坐标为![]() ;
;
当![]() 在二次函数图像上时,
在二次函数图像上时,
则点![]() 的坐标为
的坐标为![]()
 ,
,
解得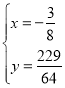
即点![]() 的坐标为
的坐标为![]()
综上可知点![]() 的坐标为
的坐标为![]() 或
或![]()

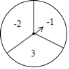
【题目】某市一研究机构为了了解![]() 岁年龄段市民对创建文明城市的关注程度,随机选取了
岁年龄段市民对创建文明城市的关注程度,随机选取了![]() 名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
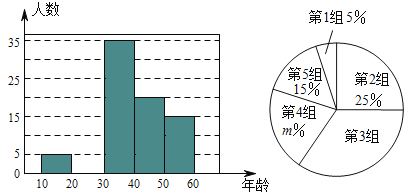
(1)请直接写出![]() ,第
,第![]() 组人数在扇形统计图中所对应的圆心角是 度;
组人数在扇形统计图中所对应的圆心角是 度;
(2)请补全上面的频数分布直方图:
(3)假设该市现有![]() 岁的市民
岁的市民![]() 万人,问
万人,问![]() 岁年龄段的关注创建文明城市的人数约有多少?
岁年龄段的关注创建文明城市的人数约有多少?