题目内容
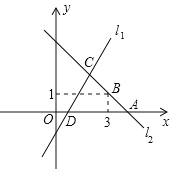
【题目】如图,正方形![]() 的边长为2,
的边长为2,![]() 为坐标原点,
为坐标原点,![]() 和
和![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,点
轴上,点![]() 是
是![]() 边的中点,过点
边的中点,过点![]() 的直线
的直线![]() 交线段
交线段![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 平分
平分![]() ,则
,则![]() 的值为__________.
的值为__________.

【答案】1或3
【解析】
分两种情况:①当点F在DC之间时,作出辅助线,求出点F的坐标即可求出k的值;②当点F与点C重合时求出点F的坐标即可求出k的值.
解:①如图,作AG⊥EF交EF于点G,连接AE,

∵AF平分∠DFE,
∴DA=AG=2,
在Rt△ADF和Rt△AGF中,![]()
∴Rt△ADF≌Rt△AGF(HL)
∴DF=FG,
∴点E是BC边的中点,
∴BE=CE=1,
∵在Rt△FCE中,EF2=FC2+CE2,
即(DF+1)2=(2-DF)2+1,
解得:DF=![]() ,
,
∴点F (![]() ,2)
,2)
把点F的坐标代入![]() 得:2=
得:2=![]() k,解得k=3
k,解得k=3
②当点F与点C重合时,
∵四边形ABCD是正方形,∴AF平分∠DFE
∴F(2,2)
把点F的坐标代入![]() 得:2=2k,解得k=1
得:2=2k,解得k=1
故答案为:1或3

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目