题目内容
9.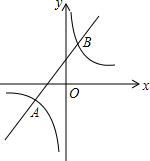 已知A(n,-2),B(2,3)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$图象的两个交点
已知A(n,-2),B(2,3)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$图象的两个交点(1)求反比例函数和一次函数的表达式;
(2)观察图象,直接写出当y2<y1时,自变量x的取值范围-3<x<0或x>2.
分析 (1)先根据反比例函数图象上点的坐标特征,把B点坐标代入y2=$\frac{m}{x}$可得m=6,从而得到反比例函数解析式,再把A(n,-2)代入反比例函数解析式求出n的值,然后利用待定系数法求一次函数解析式;
(2)观察函数图象,找出一次函数图象都在反比例函数图象的上方所对应的自变量的取值范围即可.
解答 解:(1)把B(2,3)代入y2=$\frac{m}{x}$得m=2×3=6,
所以反比例函数解析式为y2=$\frac{6}{x}$;
把A(n,-2)代入y2=$\frac{6}{x}$得-2n=6,解得n=-3,则A(-3,-2),
把A(-3,-2),B(2,3)代入y1=kx+b得$\left\{\begin{array}{l}{-3k+b=-2}\\{2k+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
所以一次函数解析式为y1=x+1;
(2)当-3<x<0或x>2时,y2<y1.
故答案为-3<x<0或x>2.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法求一次函数解析式.

练习册系列答案
相关题目
19.若x=1是一元二次方程(x+1)2-a(x+1)-2=0的一个根,则a的值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
20.下列函数中,是一次函数但不是正比例函数的是( )
| A. | y=2x | B. | y=$\frac{1}{x}$+2 | C. | y=$\frac{1}{3}$-$\frac{1}{2}$x | D. | y=2x2-1 |
17.“端午节”前夕,为保证绿色食品供应,我市准备组织20辆汽车到外地购进黄瓜、豆角、西红柿三种蔬菜共100吨.按计划20辆车都要装运,每辆汽车只能装运同一种蔬菜且必须装满.根据表格提供的信息,解答下列问题.
(1)设装运黄瓜的车辆数为x,装运豆角的车辆数为y,求y与x之间的函数关系式;
(2)如果装运黄瓜的车辆数不少于5辆,装运豆角的车辆数不少于4辆,那么,车辆的安排有几种方案?并写出每种安排方案?
(3)在(2)的条件下,应采用哪种方案才能使总运费W最少?并求出最少总运费W.
| 蔬菜种类 | 黄瓜 | 豆角 | 西红柿 |
| 每辆汽车运载量/吨 | 6 | 5 | 4 |
| 每吨所需运费/元/吨 | 120 | 160 | 180 |
(2)如果装运黄瓜的车辆数不少于5辆,装运豆角的车辆数不少于4辆,那么,车辆的安排有几种方案?并写出每种安排方案?
(3)在(2)的条件下,应采用哪种方案才能使总运费W最少?并求出最少总运费W.
1.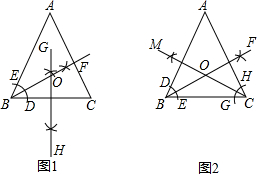 △ABC中,AB=AC,在△ABC内求作一点O,使点O到三边的距离相等.甲同学的作法如图1所示,乙同学的作法如图2所示,对于两
△ABC中,AB=AC,在△ABC内求作一点O,使点O到三边的距离相等.甲同学的作法如图1所示,乙同学的作法如图2所示,对于两
人的作法,下列说法正确的是( )
 △ABC中,AB=AC,在△ABC内求作一点O,使点O到三边的距离相等.甲同学的作法如图1所示,乙同学的作法如图2所示,对于两
△ABC中,AB=AC,在△ABC内求作一点O,使点O到三边的距离相等.甲同学的作法如图1所示,乙同学的作法如图2所示,对于两人的作法,下列说法正确的是( )
| A. | 两人都对 | B. | 两人都不对 | C. | 甲对,乙不对 | D. | 乙对,甲不对 |
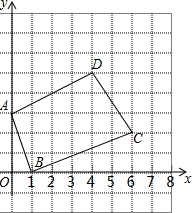 在直角坐标系中,四边形ABCD顶点的位置如图所示.
在直角坐标系中,四边形ABCD顶点的位置如图所示. 如图,在?ABCD中,对角线AC与BD相交于点O,则图中共有4对全等三角形.
如图,在?ABCD中,对角线AC与BD相交于点O,则图中共有4对全等三角形.