题目内容
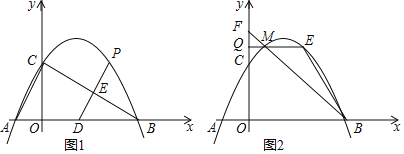
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,经过
,经过![]() 、
、![]() 两点的抛物线
两点的抛物线![]() 与
与![]() 轴的另一交点
轴的另一交点![]() .
.
(1)求该抛物线的函数表达式;
(2)![]() 是该抛物线上的动点,过点
是该抛物线上的动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①求出四边形![]() 的周长
的周长![]() 与
与![]() 的函数表达式,并求
的函数表达式,并求![]() 的最大值;
的最大值;
②当![]() 为何值时,四边形
为何值时,四边形![]() 是菱形;
是菱形;
③是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出满足条件的点
相似?若存在,请求出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①当
;(2)①当![]() 时,
时,![]() 的最大值为
的最大值为![]() ;②当
;②当![]() 时,四边形
时,四边形![]() 是菱形.③点
是菱形.③点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求二次函数的解析式,设二次函数的解析式:![]() ,根据题意求出
,根据题意求出![]() ,
,![]() 并代入
并代入![]() 求出a即可.
求出a即可.
(2)①设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,即可求出
,即可求出![]() .再根据平行线所截线段对应成比例得到
.再根据平行线所截线段对应成比例得到![]() ,用t表示CE,得
,用t表示CE,得 ![]() .再根据平行四边形的判定与性质,可以得到
.再根据平行四边形的判定与性质,可以得到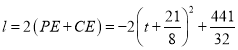 ,根据二次函数的最值即可得答案;
,根据二次函数的最值即可得答案;
②要使四边形![]() 是菱形,必有
是菱形,必有![]() ,即
,即![]() ,解出t值即可;
,解出t值即可;
③分两种情况讨论:(Ⅰ)当![]() 时,
时,![]()
![]()
![]() ,求出对应P坐标即可;(Ⅱ)当
,求出对应P坐标即可;(Ⅱ)当![]() 时,
时,![]()
![]()
![]() ,求出对应P坐标即可.
,求出对应P坐标即可.
(1)直线![]() 与
与![]() 轴、
轴、![]() 轴的交点坐标分别为
轴的交点坐标分别为![]() 、
、![]() .
.
∵抛物线与![]() 轴的另一交点
轴的另一交点![]() .
.
∴设所求抛物线的函数表达式为![]() ,
,
把点![]() 代入,得
代入,得![]() ,解得
,解得![]() .
.
∴所求抛物线的函数表达式为![]() ,
,
即![]() .
.
(2)①设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
∴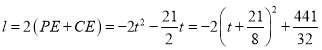 .
.
∵![]() ,
,
∴当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
②要使四边形![]() 是菱形,必有
是菱形,必有![]() ,
,
∴![]() ,整理得
,整理得![]() ,解得
,解得![]() ,
,![]() (舍去).
(舍去).
∴当![]() 时,四边形
时,四边形![]() 是菱形.
是菱形.
③分两种情况讨论:
(Ⅰ)如下图,当![]() 时,
时,![]()
![]()
![]() ,
,

∵![]() ,
,![]()
∴![]() 轴.
轴.
∴![]() ,即
,即![]() .解得
.解得![]() ,
,![]() (舍去) .
(舍去) .
∴点![]() 的坐标为
的坐标为![]() .
.
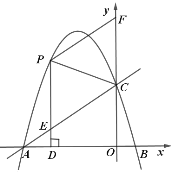
(Ⅱ)如下图,过点![]() 作
作![]() 轴于点
轴于点![]() ,当
,当![]() 时,
时,![]()
![]()
![]() ,
,
∵![]()
∴![]()
又∵![]()
∴![]()
∵![]()
∴![]()
![]()
![]() ,
,
∴![]() ,即
,即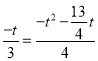 ,解得
,解得![]() ,
,![]() (舍去).
(舍去).
∴点![]() 的坐标为
的坐标为![]() .
.
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目