题目内容
 如图,已知抛物线y=
如图,已知抛物线y=| k |
| 8 |
| ||
| 3 |
(1)若点D的横坐标为-5,求抛物线的函数表达式;
(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
考点:二次函数综合题
专题:代数几何综合题,压轴题
分析:(1)首先求出点A、B坐标,然后求出直线BD的解析式,求得点D坐标,代入抛物线解析式,求得k的值;
(2)因为点P在第一象限内的抛物线上,所以∠ABP为钝角.因此若两个三角形相似,只可能是△ABC∽△APB或△ABC∽△PAB.如答图2,按照以上两种情况进行分类讨论,分别计算;
(3)由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+
DF.如答图3,作辅助线,将AF+
DF转化为AF+FG;再由垂线段最短,得到垂线段AH与直线BD的交点,即为所求的F点.
(2)因为点P在第一象限内的抛物线上,所以∠ABP为钝角.因此若两个三角形相似,只可能是△ABC∽△APB或△ABC∽△PAB.如答图2,按照以上两种情况进行分类讨论,分别计算;
(3)由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)抛物线y=
(x+2)(x-4),
令y=0,解得x=-2或x=4,
∴A(-2,0),B(4,0).
∵直线y=-
x+b经过点B(4,0),
∴-
×4+b=0,解得b=
,
∴直线BD解析式为:y=-
x+
.
当x=-5时,y=3
,
∴D(-5,3
).
∵点D(-5,3
)在抛物线y=
(x+2)(x-4)上,
∴
(-5+2)(-5-4)=3
,
∴k=
.
∴抛物线的函数表达式为:y=
(x+2)(x-4).
(2)由抛物线解析式,令x=0,得y=-k,
∴C(0,-k),OC=k.
因为点P在第一象限内的抛物线上,所以∠ABP为钝角.
因此若两个三角形相似,只可能是△ABC∽△APB或△ABC∽△PAB.

①若△ABC∽△APB,则有∠BAC=∠PAB,如答图2-1所示.
设P(x,y),过点P作PN⊥x轴于点N,则ON=x,PN=y.
tan∠BAC=tan∠PAB,即:
=
,
∴y=
x+k.
∴P(x,
x+k),代入抛物线解析式y=
(x+2)(x-4),
得
(x+2)(x-4)=
x+k,整理得:x2-6x-16=0,
解得:x=8或x=-2(与点A重合,舍去),
∴P(8,5k).
∵△ABC∽△APB,
∴
=
,即
=
,
解得:k=
.
②若△ABC∽△PAB,则有∠ABC=∠PAB,如答图2-2所示.
与①同理,可求得:k=
.
综上所述,k=
或k=
.
(3)如答图3,由(1)知:D(-5,3
),
如答图2-2,过点D作DN⊥x轴于点N,则DN=3
,ON=5,BN=4+5=9,
∴tan∠DBA=
=
=
,
∴∠DBA=30°.

过点D作DK∥x轴,则∠KDF=∠DBA=30°.
过点F作FG⊥DK于点G,则FG=
DF.
由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+
DF,
∴t=AF+FG,即运动的时间值等于折线AF+FG的长度值.
由垂线段最短可知,折线AF+FG的长度的最小值为DK与x轴之间的垂线段.
过点A作AH⊥DK于点H,则t最小=AH,AH与直线BD的交点,即为所求之F点.
∵A点横坐标为-2,直线BD解析式为:y=-
x+
,
∴y=-
×(-2)+
=2
,
∴F(-2,2
).
综上所述,当点F坐标为(-2,2
)时,点M在整个运动过程中用时最少.
| k |
| 8 |
令y=0,解得x=-2或x=4,
∴A(-2,0),B(4,0).
∵直线y=-
| ||
| 3 |
∴-
| ||
| 3 |
4
| ||
| 3 |
∴直线BD解析式为:y=-
| ||
| 3 |
4
| ||
| 3 |
当x=-5时,y=3
| 3 |
∴D(-5,3
| 3 |
∵点D(-5,3
| 3 |
| k |
| 8 |
∴
| k |
| 8 |
| 3 |
∴k=
8
| ||
| 9 |
∴抛物线的函数表达式为:y=
8
| ||
| 9 |
(2)由抛物线解析式,令x=0,得y=-k,
∴C(0,-k),OC=k.
因为点P在第一象限内的抛物线上,所以∠ABP为钝角.
因此若两个三角形相似,只可能是△ABC∽△APB或△ABC∽△PAB.

①若△ABC∽△APB,则有∠BAC=∠PAB,如答图2-1所示.
设P(x,y),过点P作PN⊥x轴于点N,则ON=x,PN=y.
tan∠BAC=tan∠PAB,即:
| k |
| 2 |
| y |
| x+2 |
∴y=
| k |
| 2 |
∴P(x,
| k |
| 2 |
| k |
| 8 |
得
| k |
| 8 |
| k |
| 2 |
解得:x=8或x=-2(与点A重合,舍去),
∴P(8,5k).
∵△ABC∽△APB,
∴
| AC |
| AB |
| AB |
| AP |
| ||
| 6 |
| 6 | ||
|
解得:k=
4
| ||
| 5 |
②若△ABC∽△PAB,则有∠ABC=∠PAB,如答图2-2所示.
与①同理,可求得:k=
| 2 |
综上所述,k=
4
| ||
| 5 |
| 2 |
(3)如答图3,由(1)知:D(-5,3
| 3 |
如答图2-2,过点D作DN⊥x轴于点N,则DN=3
| 3 |
∴tan∠DBA=
| DN |
| BN |
3
| ||
| 9 |
| ||
| 3 |
∴∠DBA=30°.

过点D作DK∥x轴,则∠KDF=∠DBA=30°.
过点F作FG⊥DK于点G,则FG=
| 1 |
| 2 |
由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+
| 1 |
| 2 |
∴t=AF+FG,即运动的时间值等于折线AF+FG的长度值.
由垂线段最短可知,折线AF+FG的长度的最小值为DK与x轴之间的垂线段.
过点A作AH⊥DK于点H,则t最小=AH,AH与直线BD的交点,即为所求之F点.
∵A点横坐标为-2,直线BD解析式为:y=-
| ||
| 3 |
4
| ||
| 3 |
∴y=-
| ||
| 3 |
4
| ||
| 3 |
| 3 |
∴F(-2,2
| 3 |
综上所述,当点F坐标为(-2,2
| 3 |
点评:本题是二次函数压轴题,难度很大.第(2)问中需要分类讨论,避免漏解;在计算过程中,解析式中含有未知数k,增加了计算的难度,注意解题过程中的技巧;第(3)问中,运用了转化思想使得试题难度大大降低,需要认真体会.

练习册系列答案
相关题目
小明和小莉出生于2013年12月份,他们的出生日不是同一天,但都是星期五,且小明比小莉出生早,两人出生日期之和是33,那么小莉的出生日期是( )
| A、18号 | B、19号 |
| C、20号 | D、21号 |
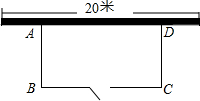 某养鸡专业户计划用一段长为35米的竹篱笆围成一个一边靠墙的矩形养鸡场地,如图,墙长20米,BC边有一个宽为1米的木门(木门用其它材料做不点用竹篱笆).设养鸡场AB边的长为x米,BC边的长为y米,BC的长度不小于10米且不超过墙长.求y关于x的函数解析式及x的取值范围.
某养鸡专业户计划用一段长为35米的竹篱笆围成一个一边靠墙的矩形养鸡场地,如图,墙长20米,BC边有一个宽为1米的木门(木门用其它材料做不点用竹篱笆).设养鸡场AB边的长为x米,BC边的长为y米,BC的长度不小于10米且不超过墙长.求y关于x的函数解析式及x的取值范围. 如图,四个一样大小的小矩形拼成一个大矩形,如果大矩形的周长为12cm,求小矩形的周长.
如图,四个一样大小的小矩形拼成一个大矩形,如果大矩形的周长为12cm,求小矩形的周长. 如图,在△ABC中,AF=2BF,CE=3AE,CD=2BD.连接CF交DE于P点,求DP、EP的比值.
如图,在△ABC中,AF=2BF,CE=3AE,CD=2BD.连接CF交DE于P点,求DP、EP的比值.