题目内容
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边作如图所示的正方形CDEF,连接AF并延长交x轴的正半轴于点B,连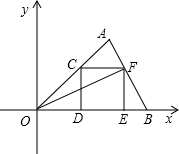 接OF,设OD=t.
接OF,设OD=t.(1)tan∠AOB=
(2)用含t的代数式表示OB的长;
(3)当t为何值时,△BEF与△OFE相似?
分析:(1)根据A点坐标,易求得tan∠AOB=1,则∠AOB=45°,△COD是等腰直角三角形,即CD=OD=DE,因此tan∠FOB=
.
(2)过A作AM⊥x轴于M,则AM=OM=2,可用t分别表示出OE、ME、EF的长,通过证△BEF∽△BMA,根据所得比例线段即可求出BE的表达式,进而可得到OB的表达式.
(3)要分两种情况进行讨论:
①∠FOE=∠FBE,此时△BFE≌△OFE,可得出OE=BE,那么OB=2OE=4OD,再根据(2)的结果即可得出t的值;②∠OFE=∠FBE,此时EF2=OE•BE,据此可表示出BE的长,而后仿照①的解法求出t的值.
| 1 |
| 2 |
(2)过A作AM⊥x轴于M,则AM=OM=2,可用t分别表示出OE、ME、EF的长,通过证△BEF∽△BMA,根据所得比例线段即可求出BE的表达式,进而可得到OB的表达式.
(3)要分两种情况进行讨论:
①∠FOE=∠FBE,此时△BFE≌△OFE,可得出OE=BE,那么OB=2OE=4OD,再根据(2)的结果即可得出t的值;②∠OFE=∠FBE,此时EF2=OE•BE,据此可表示出BE的长,而后仿照①的解法求出t的值.
解答:解:(1)1(2分),
(4分);
(2)过点A作AM⊥x轴于M,则OM=AM=2;
∵OD=t,
∴OE=2t,ME=2t-2,EF=t;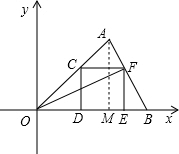
由于EF∥AM,则有△BEF∽△BMA,得:
=
,即
=
,
解得:BE=
,
故OB=OE+BE=2t+
=
.(8分)
(3)本题分两种情况:
①∠FOE=∠FBE,则有△BFE≌△OFE
∴OE=BE=2t
∴OB=4t=
,
解得t=
;
②∠OFE=∠FBE,由于△BFE∽△OFE,可得:
EF2=OE•BE,即t2=2t•BE,
∴BE=
∴OB=OE+BE=2t+
t=
t.
∴OB=
=
t,
解得t=
综上所述,当t=
或
时,△BEF与△OFE相似.
| 1 |
| 2 |
(2)过点A作AM⊥x轴于M,则OM=AM=2;
∵OD=t,
∴OE=2t,ME=2t-2,EF=t;

由于EF∥AM,则有△BEF∽△BMA,得:
| BE |
| BM |
| EF |
| AM |
| BE |
| BE+2t-2 |
| t |
| 2 |
解得:BE=
| 2t2-2t |
| 2-t |
故OB=OE+BE=2t+
| 2t2-2t |
| 2-t |
| 2t |
| 2-t |
(3)本题分两种情况:
①∠FOE=∠FBE,则有△BFE≌△OFE
∴OE=BE=2t
∴OB=4t=
| 2t |
| 2-t |
解得t=
| 3 |
| 2 |
②∠OFE=∠FBE,由于△BFE∽△OFE,可得:
EF2=OE•BE,即t2=2t•BE,
∴BE=
| t |
| 2 |
∴OB=OE+BE=2t+
| 1 |
| 2 |
| 5 |
| 2 |
∴OB=
| 2t |
| 2-t |
| 5 |
| 2 |
解得t=
| 6 |
| 5 |
综上所述,当t=
| 6 |
| 5 |
| 3 |
| 2 |
点评:此题主要考查了正方形的性质以及相似三角形的判定和性质;要注意的是(3)题中,一定要根据相似三角形的不同对应边分类讨论,同时还要注意t的取值范围,以免造成漏解或多解.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
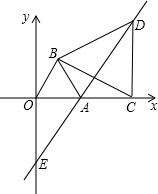 OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.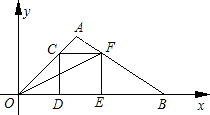 在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.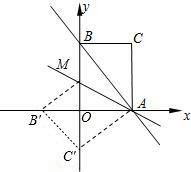 点B′处,C的对应点为C′.
点B′处,C的对应点为C′.