Question

阅读理解题： 如图，在△ABC中，AD是BC边上的中线，且AD=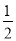BC．

求证：∠BAC=90°．

证明：∵AD=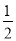BC，BD=CD=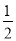BC，

∴AD=BD=DC，

∴ADB和 ADC都是等腰三角形

∴∠B=∠BAD，∠C=∠CAD，

∵∠B+∠BAD+∠CAD+∠C=180°，

∴∠BAD+∠CAD=90°，即∠BAC=90°．

（1）此题实际上是直角三角形的另一个判定方法，请你用文字语言叙述出来．

（2）直接运用这个结论解答题目：一个三角形一边长为2，这边上的中线长为1，另两边之和为1+，求这个三角形的面积．

【知识储备：勾股定理：在直角三角形中。两直角边的平方和等于斜边的平方。】

 

Answer 1

（1）如果一个三角形的一边上的中线的长等于这条边长的一半，那么这个三角形是直角三角形.（2）。

【解析】

试题分析：根据题目的已知条件和结论写出判断方法即可．

试题解析：（1）如果一个三角形的一边上的中线的长等于这条边长的一半，那么这个三角形是直角三角形。

（2）因为这个三角形的一条边上的中线长是这条边长的一半，所以这个三角形是直角三角形。

设这个直角三角形的两条直角边的长分别为a、b，则a+b=1+

根据勾股定理，得

a2+b2=22

a2+b2=4

因为（a+b）2= a2+b2+2ab

即（1+）2=4+2ab

所以

所以这个三角形的面积为

考点：直角三角形斜边上的中线．