Question

（2012•汉川市模拟）菱形ABCD的一条对角线长为6cm，边AB的长是方程x²-7x+12=0的一个根，则菱形ABCD的另一条对角线长为

2

7

cm．

Answer 1

分析：首先根据菱形的性质可得AC⊥BD，BO=

1

2

BD，AO=

1

2

AC，再解一元二次方程可得AB的长，再利用勾股定理即可计算出BO的长，进而得到BD的长．

解答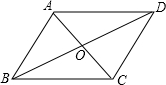：解：∵四边形ABCD是菱形，
∴AC⊥BD，AC=6，
∴AO=3，BO=

1

2

BD，
x²-7x+12=0，
（x-3）（x-4）=0，
则x-3=0，x-4=0，
解得：x₁=3（不合题意，舍去），x₂=4，
∴AB=4cm，
∴BO=

AB2-AO2

=

7

（cm），
∴BD=2

7

（cm）．
故答案为：2

7

．

点评：此题主要考查了一元二次方程的解法、菱形的性质，以及勾股定理的应用，关键是通过解一元二次方程算出AB的值．