题目内容
如图，BD是⊙O的直径，过点D的切线交⊙O的弦BC的延长线于点E，弦AC∥DE交BD于点G
（1）求证：BD平分弦AC；
（2）若弦AD＝5㎝，AC＝8㎝，求⊙O的半径.
（1）证明：∵DE是⊙O的切线，且BD是直径，∴BD⊥DE
又∵AC∥DE ∴BD⊥AC ∴BD平分AC
（2）连结AO； ∵AG=GC，AC=8cm，∴AG=4cm
在Rt△AGD中，由勾股定理得 GD=3cm
设圆的半径为r，则AO=r，OG=r-3
在Rt△AOG中，由勾股定理得 AO2=OG2+AG2
有：r2=(r-3)2+42解得 
∴⊙O的半径为cm
解析
练习册系列答案
相关题目
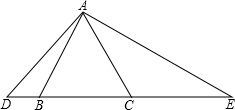如图，△ABC是一个边长为2的等边三角形，D、E都在直线BC上，并且∠DAE=120°
（2012•渝北区一模）如图，等边△ABC的边AB与正方形DEFG的边长均为2，且AB与DE在同一条直线上，开始时点B与点D重合，让△ABC沿这条直线向右平移，直到点B与点E重合为止，设BD的长为x，△ABC与正方形DEFG重叠部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（ ）
泰勒斯是古希腊哲学家，相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离．如图，B是观察点，船A在B的正前方，过B作AB的垂线，在垂线上截取任意长BD，C是BD的中点，观察者从点D沿垂直于BD的DE方向走，直到点E、船A和点C在一条直线上，那么△ABC≌△EDC，从而量出DE的距离即为船离岸的距离AB，这里判定△ABC≌△EDC的方法是（ ）
