Question

已知：如图4­3­46，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．

(1)求证：△ABM≌△DCM；

(2)判断四边形MENF是什么特殊四边形，并证明你的结论；

(3)当AD∶AB＝__________时，四边形MENF是正方形(只写结论，不需证明)．

Answer 1

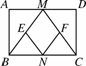
 (1)证明：在矩形ABCD中，

AB＝CD，∠A＝∠D＝90°，

又∵M是AD的中点，∴AM＝DM.

∴△ABM≌△DCM(SAS)．

(2)解：四边形MENF是菱形．证明如下：

E，F，N分别是BM，CM，CB的中点，

∴NE∥MF，NE＝MF.

∴四边形MENF是平行四边形．

由(1)，得BM＝CM，∴ME＝MF.

∴四边形MENF是菱形．

(3)2∶1　解析：当AD∶AB＝2∶1时，四边形MENF是正方形．理由：

∵M为AD中点，∴AD＝2AM.

∵AD∶AB＝2∶1，∴AM＝AB.

∵∠A＝90，∴∠ABM＝∠AMB＝45°.

同理∠DMC＝45°，∴∠EMF＝180°－45°－45°＝90°.

∵四边形MENF是菱形，∴菱形MENF是正方形．