题目内容
2.若实数a,b满足b2+a-2b+2=0,则a的取值范围是( )| A. | a≤-1 | B. | a≥-1 | C. | a≤1 | D. | a≥1 |
分析 将b2+a-2b+2=0看作关于b的一元二次方程,根据题意得到其根的判别式为非负数,据此求得a的取值范围.
解答 解:因为b是实数,所以关于b的一元二次方程是b2-2b+a+2=0,
所以△=4-4(a+2)≥0,
解得a≤-1.
故选A.
点评 本题考查了根的判别式的知识,根据根的判别式列出有关a的不等式是解题的关键.

练习册系列答案
相关题目
14.$\sqrt{6}$-3的绝对值是( )
| A. | $\sqrt{6}$-3 | B. | -$\sqrt{6}$-3 | C. | 3-$\sqrt{6}$ | D. | $\frac{1}{\sqrt{6}-3}$ |
11.在解方程$\frac{x-1}{2}$-$\frac{2x+1}{3}$=1时,去分母正确的是( )
| A. | 3(x-1)-2(2x+3)=6 | B. | 3x-3-4x+3=1 | C. | 3(x-1)-2(2x+3)=1 | D. | 3x-3-4x-2=6 |
12.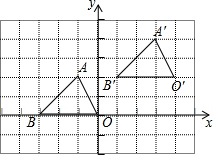 如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
 如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )| A. | (a,b) | B. | (-a,-b) | C. | (a+2,b+4) | D. | (a+4,b+2) |
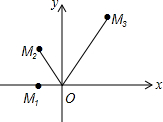 如图,在平面直角坐标系中,已知点M1(-1,0),将线段OM1绕点O按顺时针方向旋转60°,再将其长度伸长为OM1的2倍,得到线段OM2;又将线段OM2绕点O按顺时针方向旋转60°,长度伸长为OM2的2倍,得到线段OM3;如此下去,得到线段OM4,OM5…OMn(n为正整数),则点M234的坐标为(-2232,-2232•$\sqrt{3}$).
如图,在平面直角坐标系中,已知点M1(-1,0),将线段OM1绕点O按顺时针方向旋转60°,再将其长度伸长为OM1的2倍,得到线段OM2;又将线段OM2绕点O按顺时针方向旋转60°,长度伸长为OM2的2倍,得到线段OM3;如此下去,得到线段OM4,OM5…OMn(n为正整数),则点M234的坐标为(-2232,-2232•$\sqrt{3}$).