题目内容

等腰△周长为20，一边长为6，则底角的余弦值为________．

$\text{[math]}$ 或 $\text{[math]}$
分析：如图，AB=AC，AD为△ABC的高，根据等腰三角形的性质得BD= $\text{[math]}$ BC，讨论：当BC=6时，AB=AC= $\text{[math]}$ （20-6）=7，BD= $\text{[math]}$ ×6=3，根据余弦的定义得到cosB= $\text{[math]}$ = $\text{[math]}$ ；当AB=6，则AC=6，则BC=20-6-6=8，得BD= $\text{[math]}$ ×8=4，根据余弦的定义得到cosB= $\text{[math]}$ = $\text{[math]}$ ．
解答：如图，

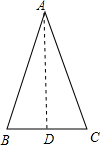AB=AC，AD为△ABC的高，
则BD= $\text{[math]}$ BC，
当BC=6时，AB=AC= $\text{[math]}$ （20-6）=7，
BD= $\text{[math]}$ ×6=3，
∴cosB= $\text{[math]}$ = $\text{[math]}$ ；
当AB=6，则AC=6，
∴BC=20-6-6=8，
∴BD= $\text{[math]}$ ×8=4，
∴cosB= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
所以此等腰三角形的底角的余弦值为 $\text{[math]}$ 或 $\text{[math]}$ ．
故答案为 $\text{[math]}$ 或 $\text{[math]}$ ．
点评：本题考查了余弦的定义：在直角三角形中，一个锐角的余弦等于这个角的邻边与斜边的比值．也考查了等腰三角形的性质以及分类讨论思想的运用．