题目内容
2.已知有理数a、b、c均不为零,求$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{abc}{|abc|}$的值.分析 根据a、b、c是非零实数,分两正一负或两负一正两种情况分别讨论求值即可.
解答 解:由已知可得:a,b,c为两正一负或两负一正.
①当a,b,c为两正一负时:$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{abc}{|abc|}$=0.
②当a,b,c为两负一正时:$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{abc}{|abc|}$=0.
③当a,b,c都为正数时:$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{abc}{|abc|}$=4.
④当a,b,c都为负数时:$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{abc}{|abc|}$=-4.
综上所述$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{abc}{|abc|}$的值为0或4或-4.
点评 本题考查了分式的化简求值,涉及到绝对值、非零实数的性质等知识点,注意分情况讨论未知数的取值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在-(-8),-|-7|,-0,(-$\frac{2}{3}$)2这四个数中,负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.(5a-3b)-3(a2-2b)等于( )
| A. | -3a2+5a+3b | B. | 2a2+3b | C. | 2a3-b2 | D. | -3a2 |
11.下列用数轴表示不等式2-x≤1的解集正确的是( )
| A. | 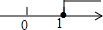 | B. |  | C. |  | D. |  |
12.为了鼓励市民节约用水,某市制定出一套节水的管理措施,对市民生活用水收费作如下规定:
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)若该户某月用水量为x吨,缴纳水费y元,试列出y关于x的函数式;
(3)若某用户七月份缴纳水费100元,该用户七月份用水量是多少?
| 月用水量(吨) | 单价(元/吨) |
| 不大于10吨部分 | 2.5 |
| 大于10吨不大于20吨部分 | 4 |
| 大于20吨部分 | 5 |
(2)若该户某月用水量为x吨,缴纳水费y元,试列出y关于x的函数式;
(3)若某用户七月份缴纳水费100元,该用户七月份用水量是多少?
 已知正比例函数y=$\frac{1}{2}$x的图象与一次函数y=kx-3的图象相交于点(2,a).
已知正比例函数y=$\frac{1}{2}$x的图象与一次函数y=kx-3的图象相交于点(2,a).