题目内容
19.如图,已知抛物线经过A(1,0)、B(0,3)两点,对称轴是x=-1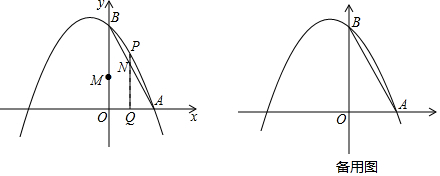
(1)求抛物线对应的函数关系式;
(2)动点Q从点O出发,以每秒1个单位长度的速度在线段OM上运动,同时动点M从M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPQ为矩形;
②△AON能否为等腰三角形?若能,直接写出t的值;若不能,请说明理由.
分析 (1)利用顶点式、待定系数法求出抛物线的解析式;
(2)①当四边形OMPQ为矩形时,满足条件OM=PQ,据此列一元二次方程求解;
②△AON为等腰三角形时,可能存在三种情形,需要分类讨论,逐一计算.
解答 解:(1)根据题意,设抛物线的解析式为:y=a(x+1)2+k,
∵点A(1,0),B(0,3)在抛物线上,
∴$\left\{\begin{array}{l}{4a+k=0}\\{a+k=3}\end{array}\right.$,
解得:a=-1,k=4,
∴抛物线的解析式为:y=-(x+1)2+4=-x2-2x+3;
(2)①∵四边形OMPQ为矩形,
∴OM=PQ,即3t=-(t+1)2+4,
整理得:t2+5t-3=0,
解得t=$\frac{-5±\sqrt{37}}{2}$,由于t=$\frac{-5-\sqrt{37}}{2}$<0,故舍去,
∴当t=$\frac{\sqrt{37}-5}{2}$秒时,四边形OMPQ为矩形;
②能,Rt△AOB中,OA=1,OB=3,∴tanA=3.
若△AON为等腰三角形,有三种情况: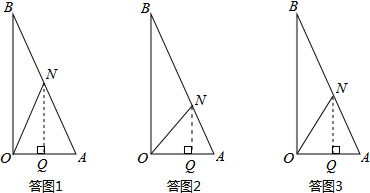
(I)若ON=AN,如答图1所示:
则Q为OA中点,OQ=$\frac{1}{2}$OA=$\frac{1}{2}$,
∴t=$\frac{1}{2}$;
(II)若ON=OA,如答图2所示:
设AQ=x,则NQ=AQ•tanA=3x,OQ=OA-AQ=1-x,
在Rt△NOQ中,由勾股定理得:OQ2+NQ2=ON2,
即(1-x)2+(3x)2=12,解得x1=$\frac{1}{5}$,x2=0(舍去),
∴x=$\frac{1}{5}$,OQ=1-x=$\frac{4}{5}$,
∴t=$\frac{4}{5}$;
(III)若OA=AN,如答图3所示:
设AQ=x,则NQ=AQ•tanA=3x,
在Rt△ANQ中,由勾股定理得:NQ2+AQ2=AN2,
即(x)2+(3x)2=12,解得x1=$\frac{\sqrt{10}}{10}$,x2=-$\frac{\sqrt{10}}{10}$(舍去),
∴OQ=1-x=1-$\frac{\sqrt{10}}{10}$,
∴t=1-$\frac{\sqrt{10}}{10}$.
当t为$\frac{1}{2}$秒、$\frac{4}{5}$秒,(1-$\frac{\sqrt{10}}{10}$)秒时,△AON为等腰三角形.
点评 本题考查了二次函数的图象与性质、待定系数法、解一元二次方程、勾股定理、解直角三角形、矩形性质、等腰三角形的性质等知识点,综合性比较强,有一定的难度.第(2)问为运动型与存在型的综合性问题,注意要弄清动点的运动过程,进行分类讨论计算.

 口算能手系列答案
口算能手系列答案| A. |  | B. |  | C. |  | D. |  |
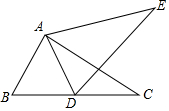 如图,将△ABC绕点A逆时针旋转50°得到△ADE,其中点D恰好落在BC边上,则∠EDC等于( )
如图,将△ABC绕点A逆时针旋转50°得到△ADE,其中点D恰好落在BC边上,则∠EDC等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 65° |
| A. | 1 | B. | 6 | C. | 1或6 | D. | 5或6 |
 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.



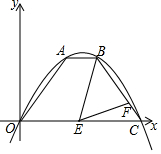 如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.
如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.