题目内容
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
(1) 在网格中画出△AB1C1;
(2) 计算点B旋转到B1的过程中所经过的路径长.(结果保留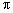 )
)
 |
.解:(1)画出△AB1C1,如图. ……………………………………2分
(2)由图可知△ 是直角三角形,AC=4,BC=3,
是直角三角形,AC=4,BC=3,
 所以AB=5. ……………………………………3分
所以AB=5. ……………………………………3分
点B旋转到B1的过程中所经过的路径是一段弧,
且它的圆心角为90°,半径为5. …………4分
∴ =
= . …………5分
. …………5分
所以点B旋转到B1的过程中所经过的路径长为 .
.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案阅读下面材料:
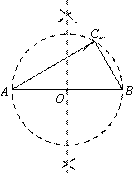
在数学课上,老师提出如下问题:
|

小芸的作法如下:
|
老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是 .
有这样一个问题:探究函数 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1) 函数 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2) 下表是y与x的几组对应值.
| x | … |
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | 5 | … |
| y | … |
|
|
|
|
|
|
|
| 3 |
| m |
| … |
求m的值;
(3) 如下图,在平面直角坐标系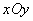 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(4) 进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):
.
下列现象:
(1)用两个钉子就可以把木条固定在墙上.
(2)从A地到B地架设电线,总是尽可能沿着线段AB架设.
(3)植树时,只要确定两棵树的位置,就能确定同一行树所在的直线.
(4)把弯曲的公路改直,就能缩短路程.
其中能用“两点确定一条直线”来解释的现象有( )
| A. (1)(2) | B. (1)(3) | C. (2)(4) | D. (3)(4) |
 的值为
的值为 D. 1
D. 1 
 是栏杆转动的支点,点
是栏杆转动的支点,点 是栏杆两段的联结点.当车辆经过时,栏杆
是栏杆两段的联结点.当车辆经过时,栏杆 最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:
最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据: ≈1.4)
≈1.4)




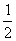











 是关于x的方程4x+m=3的解,那么m的值是
是关于x的方程4x+m=3的解,那么m的值是 C.-1 D.
C.-1 D. 
