题目内容
有这样一个问题:探究函数 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1) 函数 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2) 下表是y与x的几组对应值.
| x | … |
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | 5 | … |
| y | … |
|
|
|
|
|
|
|
| 3 |
| m |
| … |
求m的值;
(3) 如下图,在平面直角坐标系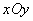 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(4) 进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):
.
解:(1) . ……………………………………1分
. ……………………………………1分
(2)当 时,
时, ,
,
 ∴
∴ . ……………………………………2分
. ……………………………………2分
(3)该函数的图象如右图所示.
……………………………4分
(4) 该函数的其它性质:
①当 时,y随x的增大而增大;
时,y随x的增大而增大;
当 时,y随x的增大而减小;
时,y随x的增大而减小;
当 时,y随x的增大而增大.
时,y随x的增大而增大.
②函数的图象不经过第二象限.
③函数的图象与x轴无交点,图象由两部分组成.
④函数的图象关于点(1,1)成中心对称.
……(写出一条即可) ……………………………………5分

练习册系列答案
相关题目



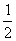














 油桶制造厂的某车间生产圆形铁片和长方形铁片,如图,两个圆形铁片和一个长方形铁片可以制造成一个油桶.已知该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.问安排生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?
油桶制造厂的某车间生产圆形铁片和长方形铁片,如图,两个圆形铁片和一个长方形铁片可以制造成一个油桶.已知该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.问安排生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套? 15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)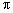 )
)
 元提高50%标价,然后再以8折优惠卖出,则这种旅游鞋每双的售价是
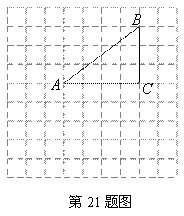
元提高50%标价,然后再以8折优惠卖出,则这种旅游鞋每双的售价是 直线CD上确定一点O,使点O到村庄A,B的距离之和最小,
直线CD上确定一点O,使点O到村庄A,B的距离之和最小, 的倒数是 ,相反数是 .
的倒数是 ,相反数是 .