Question

【题目】已知，当时，．

（1）求这个函数的表达式；

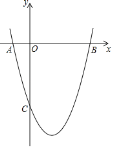
（2）在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质；

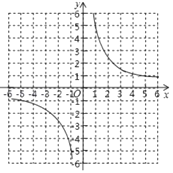
（3）已知函数的图象如图所示，结合你所画的函数图象，直接写出不等式的解集．

Answer 1

【答案】（1）；（2）当时，随的增大而增大；当时随的增大而减小；（3）或．

【解析】

（1）将x=1，y=5代入可求得k的值；

（2）将函数写成分段函数的形式，然后分别画每一段函数图形；

（3）读图，分段函数的图像比反比例函数图像高的部分即为解集

解：（1）∵在函数中，当时，，

∴，解得，∴这个函数的表达式是；

（2）∵，

∴，∴该函数的图象如图所示：

由图象可知：当时，随的增大而增大；当时随的增大而减小；

（3）由函数图象可得：

不等式的解集是或．