题目内容
4.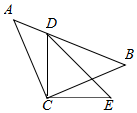 如图,AC=BC且AC⊥BC,点D在AB上,DC=EC且DC⊥EC.
如图,AC=BC且AC⊥BC,点D在AB上,DC=EC且DC⊥EC.求证:AD2+BD2=2EC2.
分析 连接BE,由等腰直角三角形的性质得出∠A=∠ABC=45°,∠ACB=∠DCE=90°,证出∠ACD=∠BCE,由SAS证明△ACD≌△BCE,得出BE=AD,∠EBC=∠A=45°,求出∠DBE=90°,在Rt△BDE和Rt△CDE中,由勾股定理得出BD2+BE2=CD2+EC2,即可得出结论.
解答 证明:连接BE,如图所示: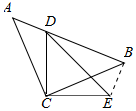
∵AC=BC且AC⊥BC,DC=EC且DC⊥EC,
∴∠A=∠ABC=45°,∠ACB=∠DCE=90°,
∴∠ACB-∠BCD=∠DCE-∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACD=∠BCE}&{\;}\\{DC=EC}&{\;}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴BE=AD,∠EBC=∠A=45°,
∴∠DBE=45°+45°=90°,
在Rt△BDE和Rt△CDE中,DE2=BD2+BE2,DE2=CD2+EC2,
∴BD2+BE2=CD2+EC2,
又∵AD=BE,CD=EC,
∴AD2+BD2=2EC2.
点评 本题考查了勾股定理、等腰直角三角形的性质、全等三角形的判定与性质;熟练掌握勾股定理,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
17.已知$\root{3}{374}$≈7.205,$\root{3}{37.4}$≈3.344,则$\root{3}{-0.000374}$约等于( )
| A. | -0.07205 | B. | -0.03344 | C. | -0.07205 | D. | -0.003344 |
18.以下说法正确的是( )
| A. | 若$\sqrt{x-1}$+$\sqrt{1-x}$=y+4,则xy的平方根为1 | B. | 3-2$\sqrt{2}$的绝对值是2$\sqrt{2}$-3 | ||
| C. | 若$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$成立,则a≤0且b≥0 | D. | 若$\sqrt{(1-a)^{2}}$+$\sqrt{(a-3)^{2}}$=2,则a≥3 |
15.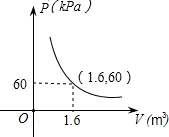 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )| A. | 不小于$\frac{5}{4}$ m3 | B. | 小于$\frac{5}{4}$ m3 | C. | 不小于$\frac{4}{5}$ m3 | D. | 小于$\frac{4}{5}$ m3 |
13.函数y=$\frac{k}{x}$的图象经过点(-4,6),则下列各点中在y=$\frac{k}{x}$图象上的是( )
| A. | (3,8) | B. | (3,-8) | C. | (-8,-3) | D. | (-4,-6) |