Question

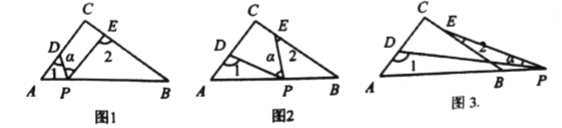
【题目】如图：点C在线段BD上，AC⊥CE，∠A=∠1，∠E=∠2．

(1)若∠1=70°，求∠B、∠D的度数；

(2)判断AB与ED的位置关系，并说明理由；

(3)作∠A、∠E的角平分线相交于点P，求∠P的度数．

Answer 1

【答案】（1），；（2），证明见解析；（3）．

【解析】

（1）由三角形内角和及已知直接可求∠B ，再AC⊥CE可得，求出∠2，同理可求∠D．

（2）由已知易得，从而可得，根据平行线的判定定理得到：直线与平行．

（3）由AP、EP是∠BAC、∠CED的角平分线可得，再由三角形内角和定理可求，进而可得，再由三角形内角和即可求解．

解：（1）∵∠A=∠1，∠1=70°，

在中，，

∴，

又，

∴，

又∵，，

．

（2）；理由如下：

，

∴，

又∵∠A=∠1，∠E=∠2．

∴

∴，

又∵，

，

．

（3）如图，连接AE，

由（2）可知，

∵AP、EP平分、，即，

∴，

，

∴，

∴，

∴，

即：．