题目内容
 完成下面的证明.
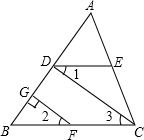
完成下面的证明.已知,如图,∠AED=∠ACB,∠1=∠2,FG⊥AB于G,求证:CD⊥AB.
证明:∵∠AED=∠ACB(已知)
∴DE∥BC(
∴∠1=∠3(
又∵∠1=∠2(已知)
∴∠2=∠3(
∴DC∥GF(
∴∠BGF=∠CDB(
∵FG⊥AB(已知)
∴∠BGF=90°(
∴∠CDB=90°(
∴CD⊥AB(
考点:平行线的判定与性质,垂线
专题:推理填空题
分析:根据平行线的性质定理和判定定理即可解答.
解答:证明:∵∠AED=∠ACB(已知)
∴DE∥BC( 同位角相等,两直线平行)
∴∠1=∠3( 两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴∠2=∠3( 等量代换)
∴DC∥GF( 同位角相等,两直线平行)
∴∠BGF=∠CDB( 两直线平行,同位角相等)
∵FG⊥AB(已知)
∴∠BGF=90°( 垂直的定义)
∴∠CDB=90°( 等量代换)
∴CD⊥AB( 垂直的定义).
∴DE∥BC( 同位角相等,两直线平行)
∴∠1=∠3( 两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴∠2=∠3( 等量代换)
∴DC∥GF( 同位角相等,两直线平行)
∴∠BGF=∠CDB( 两直线平行,同位角相等)
∵FG⊥AB(已知)
∴∠BGF=90°( 垂直的定义)
∴∠CDB=90°( 等量代换)
∴CD⊥AB( 垂直的定义).
点评:本题考查了平行线的性质定理和判定定理,理解定理是关键.

练习册系列答案
相关题目
函数y=ax-3的图象与y=bx+4的图象交于x轴上一点,那么a:b等于( )
| A、-4:3 |
| B、4:3 |
| C、(-3):(-4) |
| D、3:(-4) |
 如图,AB是⊙O的直径,C是⊙O上一点,AD⊥CD于D,BE⊥CD于E,BC平分∠ABE,连接AC、BC.
如图,AB是⊙O的直径,C是⊙O上一点,AD⊥CD于D,BE⊥CD于E,BC平分∠ABE,连接AC、BC. 画出图中的物体的三种视图.
画出图中的物体的三种视图.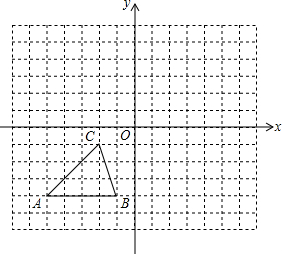 如图,方格纸中的每个小方格都是边长为1个单位的正方形,每个小正方形的顶点叫格点.已知△ABC的顶点均在格点上,在建立平面直角坐标系后,点B的坐标为l2.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,每个小正方形的顶点叫格点.已知△ABC的顶点均在格点上,在建立平面直角坐标系后,点B的坐标为l2.