题目内容
2.如图,抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(1,0)和B两点,与y轴交于C(0,2)点,点D与点C关于抛物线的对称轴l对称.连接AC,AD.(1)求抛物线的解析式.
(2)P是抛物线上一点.若∠PDA与∠OAC互余,求点P的坐标.
(3)在抛物线对称轴l上是否存在一点Q.使△QAD为直角三角形?若存在,请直接写出所有Q点坐标;若不存在,请说明理由.

分析 (1)将点A和点C的坐标代入抛物线的解析式可求得b,c的值,然后可得到抛物线的解析式;
(2)先求得抛物线与y轴的交点坐标,然后再求得抛物线的对称轴,从而可得到点D的坐标,依据两点间的距离公式可求得AC、AD、CD的长,可证明△CAD为直角三角形,故此可知∠DAB与∠CAO互余,只要角∠PDA=∠DAB即可,如图1所示当PD∥AB时,可求得点P与点C重合;如图2所示:作AD的垂直平分线交x轴与点G,作射线DG交抛物线与点P,交AD与点E.依据线段的中点坐标公式可求得点E的坐标,然后再求得EG的解析式,可得到点G的坐标,接下来,求得DG的解析式,最后将DG的解析式与抛物线的解析式联立可求得点P的坐标;
(3)设点Q的坐标为($\frac{5}{2}$,y).依据两点间的距离公式可知:AD2=(5-1)2+(2-0)2=20,AQ2=(2.5-1)2+y2,DQ2=(5-2.5)2+(y-2)2.然后分为AD2+AQ2=DQ2时;AD2+DQ2=AQ2时;当AQ2+DQ2=AD2时三种情况列方程求解即可.
解答 解:(1)将点A和点C的坐标代入抛物线的解析式得:$\left\{\begin{array}{l}{\frac{1}{2}+b+c=0}\\{c=2}\end{array}\right.$,解得:b=-$\frac{5}{2}$,c=2.
抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{5}{2}$x+2.
(2)如图1所示:
将x=0代入抛物线的解析式得:y=2,
∴点C的坐标为(0,2).
∵点C与点D关于l对称,
∴点D的坐标为(5,2).
令y=0得:
抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{5}{2}$,
∵点C与点D关于x=-$\frac{5}{2}$对称,
∴依据两点间的距离公式可知AC=$\sqrt{O{C}^{2}+A{O}^{2}}$=$\sqrt{5}$,AD=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
∵AC2+AD2=AD2,
∴△ACD为直角三角形.
∴∠CAO+∠DAB=90°.
又∵∠OCA+∠CAO=90°,
∴∠OCA=∠DAB.
∴当∠PDA=∠DAB时,∠PDA与∠OAC互余.
∵CD∥AB,
∴∠CDA=∠DAB.
∴点P与点C重合.
∴点P的坐标为(0,2).
如图2所示:作AD的垂直平分线交x轴与点G,作射线DG交抛物线与点P,交AD与点E.
∵点E是AD的中点,
∴点E的坐标为(3,1).
设AD的解析式为y=kx+b,将点A和点D的坐标代入得:$\left\{\begin{array}{l}{k+b=0}\\{5k+b=2}\end{array}\right.$,解得:k=$\frac{1}{2}$,b=-$\frac{1}{2}$.
∴直线AD的解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$.
设直线EG的解析式为y=-2x+n,将点E的坐标代入得:-6+n=1,解得n=7,
∴直线EG的解析式为y=-2x+7.
将y=0代入得:-2x+7=0,解得:x=3.5.
∴点G的坐标为(3.5,0).
设DG的解析式为y=ax+m,将D和G的坐标代入得:$\left\{\begin{array}{l}{3.5a+m=0}\\{5a+m=2}\end{array}\right.$,解得:a=$\frac{4}{3}$,m=-$\frac{14}{3}$.
∴直线DG的解析式为y=$\frac{4}{3}$x-$\frac{14}{3}$.
将y=$\frac{4}{3}$x-$\frac{14}{3}$与y=$\frac{1}{2}$x2-$\frac{5}{2}$x+2联立解得:x=5或x=$\frac{8}{3}$,
当x=$\frac{8}{3}$时,y=-$\frac{10}{9}$,
∴点P的坐标为($\frac{8}{3}$,-$\frac{10}{9}$).
∴点P的坐标为(0,2)或($\frac{8}{3}$,-$\frac{10}{9}$).
(3)设点Q的坐标为($\frac{5}{2}$,y).
依据两点间的距离公式可知:AD2=(5-1)2+(2-0)2=20,AQ2=(2.5-1)2+y2,DQ2=(5-2.5)2+(y-2)2.
当AD2+AQ2=DQ2时,(2.5-1)2+y2+20=(5-2.5)2+(y-2)2,解得:y=-3,
∴点Q的坐标为($\frac{5}{2}$,-3).
当AD2+DQ2=AQ2时,20+(5-2.5)2+(y-2)2=(2.5-1)2+y2,解得:y=7,
∴点Q的坐标为($\frac{5}{2}$,7).
当AQ2+DQ2=AD2时,(2.5-1)2+y2+(5-2.5)2+(y-2)2=20,解得:y=1±$\frac{\sqrt{19}}{2}$.
∴点Q的坐标为($\frac{5}{2}$,1+$\frac{\sqrt{19}}{2}$)或($\frac{5}{2}$,1-$\frac{\sqrt{19}}{2}$).
综上所述,点Q的坐标为($\frac{5}{2}$,-3)或($\frac{5}{2}$,7)或($\frac{5}{2}$,1+$\frac{\sqrt{19}}{2}$)或($\frac{5}{2}$,1-$\frac{\sqrt{19}}{2}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式,两点间的距离公式、勾股定理的逆定理,依据勾股定理的逆定理列出关于y的方程是解题的关键.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
| A. | -3 | B. | $\frac{1}{3}$ | C. | 3 | D. | -$\frac{1}{3}$ |
| A. | 44×105 | B. | 0.44×107 | C. | 4.4×106 | D. | 4.4×105 |
| A. | 点(1,3)关于x轴的对称点是(-1,3) | |
| B. | 函数 y=-2x+3中,y随x的增大而增大 | |
| C. | 若一组数据3,x,4,5,6的众数是3,则中位数是3 | |
| D. | 同圆中的两条平行弦所夹的弧相等 |
| A. | $\sqrt{21}$ | B. | $\sqrt{30}$ | C. | $\sqrt{47}$ | D. | $\root{3}{39}$ |




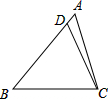 在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2$\sqrt{2}$,AB=3,则AD=$\frac{1}{3}$.
在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2$\sqrt{2}$,AB=3,则AD=$\frac{1}{3}$.