题目内容
如图,点P在双曲线 (k.>0)第一象限内的分支上运动
(k.>0)第一象限内的分支上运动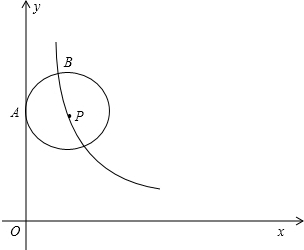 ,以P为圆心的圆保持与y轴相切于点A,与双曲线交于点B,点B在点P上方.
,以P为圆心的圆保持与y轴相切于点A,与双曲线交于点B,点B在点P上方.
(1)当点P的横坐标为2时,⊙P与y轴的切点A(0, ),试求双曲线
),试求双曲线 的解析式;
的解析式;
(2)切点A是否有可能与坐标原点O重合?
(3)在(1)的条件下,是否存在点P,使得△ABP为正三角形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
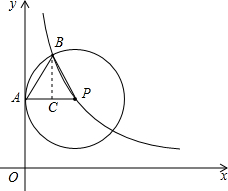 解:(1)∵点P的横坐标为2时,⊙P与y轴的切点A(0,
解:(1)∵点P的横坐标为2时,⊙P与y轴的切点A(0, ),
),∴点P的坐标为:(2,
 ),
),∴
 =
= ,
,∴k=2
 ,
,∴双曲线y=
 的解析式为:y=
的解析式为:y=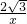 ;
;(2)切点A不能与坐标原点O重合.
理由:若切点A与坐标原点O重合,
则点P的纵坐标为0,
即点P在x轴上,
∵反比例函数与x轴不相交,
∴点P不能在x轴上,
∴切点A不能与坐标原点O重合;
(3)存在.
理由:设点P的坐标为:(a,
 ),
),则AP=a,
过点B作BC⊥AP于点C,
∵△ABP为正三角形,
∴AC=
 AP=
AP= a,∠BAP=60°,
a,∠BAP=60°,在Rt△BAC中,BC=AC•cos∠BAP=
 a×
a× =
= a,
a,∴点B的坐标为:(
 a,
a, a+
a+ ),
),∵点B在双曲线y=
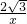 上,
上,∴
 a×(
a×( a+
a+ )=2
)=2 ,
,解得:a2=4,
∴a=±2.
∵点P在第一象限,
∴a=2,
∴点P的坐标为:(2,
 ).
).分析:(1)点P的横坐标为2时,⊙P与y轴的切点A(0,
 ),可得点P的坐标为:(2,
),可得点P的坐标为:(2, ),然后由待定系数法即可求得双曲线
),然后由待定系数法即可求得双曲线 的解析式;
的解析式;(2)利用反证法,若切点A与坐标原点O重合,可得即点P在x轴上,又由反比例函数与x轴不相交,可得切点A不能与坐标原点O重合;
(3)设点P的坐标为:(a,
 ),由△ABP为正三角形,可求得点B的坐标为:(
),由△ABP为正三角形,可求得点B的坐标为:( a,
a, a+
a+ ),又由点B在双曲线y=
),又由点B在双曲线y=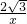 上,即可得方程
上,即可得方程 a×(
a×( a+
a+ )=2
)=2 ,解此方程即可求得a的值,继而求得答案.
,解此方程即可求得a的值,继而求得答案.点评:此题考查了待定系数法求反比例函数的解析式、切线的性质、正三角形的性质以及点与反比例函数的性质.此题难度较大,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点A在双曲线y=
如图,点A在双曲线y=| 6 |
| x |
A、2
| ||
| B、5 | ||
C、4
| ||
D、
|
 如图,点A在双曲线
如图,点A在双曲线 (2012•镇赉县模拟)如图,点P在双曲线
(2012•镇赉县模拟)如图,点P在双曲线 (2012•三明)如图,点A在双曲线
(2012•三明)如图,点A在双曲线 如图,点A在双曲线
如图,点A在双曲线