题目内容
如图，在?ABCD中，E为BC的中点，DE⊥AE，求证：AD=2AB．考点：矩形的性质,全等三角形的判定与性质
专题：证明题
分析：如图，作辅助线；证明AB=CD；AE=EF，AB=CF；得到AD=DF，即可解决问题．
解答：
证明：分别延长AE、DC交于点F；
∵四边形ABCD为平行四边形，
∴AB∥CF，DC=AB；
∴△ABE∽△FCE，
∴AE：EF=BE：CE=AB：CF；
∵E为BC的中点，
∴BE=CE，
∴AE=FE，AB=CF，
∴DE为AF的中垂线，
∴AD=DF=2AB．
证明：分别延长AE、DC交于点F；∵四边形ABCD为平行四边形，
∴AB∥CF，DC=AB；
∴△ABE∽△FCE，
∴AE：EF=BE：CE=AB：CF；
∵E为BC的中点，
∴BE=CE，
∴AE=FE，AB=CF，
∴DE为AF的中垂线，
∴AD=DF=2AB．
点评：该题主要考查了平行四边形的性质、相似三角形的判定及其性质、线段的垂直平分线的性质等几何知识点的应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是 （ ）
| A、无限小数都是无理数 |
| B、无理数的相反数还是无理数 |
| C、正数、负数统称有理数 |
| D、两个无理数的和一定是无理数 |
如图，已知A，B，C，D四个点，请按要求画图：
如图，l1∥l2∥l3，试证明：在⊙O中，弦AB所对的圆心角是40°，弦AB所对的圆周角是（ ）
| A、20° |
| B、80° |
| C、20°或160° |
| D、80°或100° |
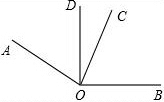如图，OC平分∠AOB，∠BOD=2∠AOD．
如图，在四边形ABCD中，E、F分别是AD、BC的中点，连接FE并延长，分别交CD的延长线于点M、N，∠BME=∠CNE，求证：AB=CD．