题目内容
过正方形ABCD的顶点A任引一直线交BC和DC的延长线于P、Q.求证: 为定值.
为定值.
 证明:如图:设正方形的边长为a,BP=x,则CP=a-x,
证明:如图:设正方形的边长为a,BP=x,则CP=a-x,∵△ABP∽△QCP,∴
 =
=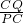 ,即:
,即: =
= ,得:CQ=
,得:CQ= .
.PQ2=PC2+CQ2=(a-x)2+
 =
= .
.∵
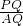 =
=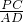 =
=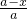 ,∴
,∴ =
= .
.又
 =
=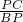 =
=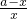 ,∴
,∴ =
= .
.∴
 +
+ =
= +
+ =
= .
.∴
 +
+ =
= •
• =
= •
• =
= .
.而a是正方形的边长,所以
 +
+ 为定值.
为定值.分析:首先设正方形的边长为a,BP的长为x,根据相似三角形对应边的比相等,用含a和x的式子表示CQ,然后用勾股定理求出PQ2,再运用相似三角形对应边的比表示出
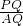 和
和 ,进行计算证明得到
,进行计算证明得到 +
+ 的值是一个定值,是正方形边长的平方分之一.
的值是一个定值,是正方形边长的平方分之一.点评:本题考查的是相似三角形的判定与性质,根据正方形的对边平行且相等,得到相似三角形,运用相似三角形的性质,对应边的比相等进行计算,可以证明
 +
+ 为定值.
为定值. 
练习册系列答案
相关题目
 如图,过正方形ABCD的顶点B作BE∥CA,且作AE=AC又CF∥AE,则下列等式成立的是( )
如图,过正方形ABCD的顶点B作BE∥CA,且作AE=AC又CF∥AE,则下列等式成立的是( )A、∠BCF=
| ||
B、∠BCF=
| ||
C、∠BCF=
| ||
| D、∠BCF=∠BFC |
 37、如图,过正方形ABCD的顶点A作直线交BD于E,交CD于F,交BC的延长线于G.若H是FG的中点,求证:EC⊥CH.
37、如图,过正方形ABCD的顶点A作直线交BD于E,交CD于F,交BC的延长线于G.若H是FG的中点,求证:EC⊥CH.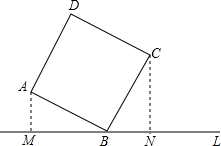 如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是
如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是 15、如图,直线l过正方形ABCD的顶点D,过A、C分别作直线l的垂线,垂足分别为E、F.若AE=4a,CF=a,则正方形ABCD的面积为
15、如图,直线l过正方形ABCD的顶点D,过A、C分别作直线l的垂线,垂足分别为E、F.若AE=4a,CF=a,则正方形ABCD的面积为 (2013•红河州)如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
(2013•红河州)如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.