Question

16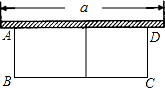．如图所示某农户打算建造一个花圃种植两种不同的花卉供应城市市场，这是需要用长为24米的篱笆靠着墙（墙的最大可用长度为a是10米），围成中间隔有道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S米²．
（1）求S与x的函数关系式？并写出x的取值范围；
（2）如果要围成面积为45m²的花圃，AB的长是多少米？
（3）花圃的面积能达到48m²吗？如果能，请求出此时AB的长；如果不能，请说明理由．

Answer 1

分析 （1）可先用篱笆的长表示出BC的长，然后根据矩形的面积=长×宽，得出S与x的函数关系式．
（2）根据（1）的函数关系式，将S=45代入其中，求出x的值即可．
（3）把（1）中用代数式表示的面积整理为a（x-h）²+b的形式可得最大的面积．

解答 解：（1）由题意可知，花圃的宽AB为x米，则BC为（24-3x）米，
这时面积S=x（24-3x）=-3x²+24x（$\frac{14}{3}$≤x＜8）．

（2）由条件-3x²+24x=45化为x²-8x+15=0，
解得x₁=5，x₂=3，
∵$\frac{14}{3}$≤x＜8，
∴x=3不合题意，舍去，
即花圃的宽为5米．

（3）花圃的面积为S=（24-3x）x=-3（x-4）²+48，
∴当AB长为4m，宽为12m时，有最大面积，为48平方米．
又∵当AB=4m时，长方形花圃的长为24-3×4=12米，
又墙的最大可用长度a是10m，故舍去；
故花圃的面积不能达到48m²．

点评 本题考查了一元二次方程，二次函数的综合应用，根据已知条件列出二次函数式是解题的关键．要注意题中自变量的取值范围不要丢掉．