题目内容
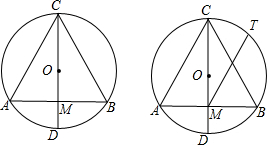
14. 姐图,△ABC是等边三角形,D为AB的中点,DE⊥AC于点E,EF∥AB交BC于点F,已知AE=5m,你能求出△EFC的周长吗?
姐图,△ABC是等边三角形,D为AB的中点,DE⊥AC于点E,EF∥AB交BC于点F,已知AE=5m,你能求出△EFC的周长吗?
分析 首先根据含30°角的直角三角形的性质求得AD的长,继而求得等边△ABC的边长,然后求得EC的长,根据平行线的性质得出∠EFC=∠B=60°,∠FEC=∠A=60°,即可证得△EFC是等边三角形,从而求得△EFC的周长.
解答 解:∵△ABC是等边三角形,
∴∠A=60°,
∵DE⊥AC,
∴∠ADE=30°,
∴AD=2AE=2×5=10m,
∵D为AB的中点,
∴AB=2AD=20m,
∴AC=AB=20m,
∴EC=AC-AE=15m,
∵EF∥AB,
∴∠EFC=∠B=60°,∠FEC=∠A=60°,
∴△EFC是等边三角形,
∴△EFC的周长=3EC=3×15=45m.
点评 本题考查了等边三角形的判定和性质,含30°角的直角三角形的性质,平行线的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
4.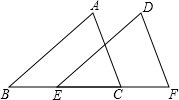 如图,已知AB=DE,BE=CF,添加下列中一个条件还不能使△ABC≌△DEF的是( )
如图,已知AB=DE,BE=CF,添加下列中一个条件还不能使△ABC≌△DEF的是( )
 如图,已知AB=DE,BE=CF,添加下列中一个条件还不能使△ABC≌△DEF的是( )
如图,已知AB=DE,BE=CF,添加下列中一个条件还不能使△ABC≌△DEF的是( )| A. | AC=DF | B. | ∠B=∠DEF | C. | ∠A=∠D=90° | D. | ∠ACB=∠F |
2.二次函数y=-3(x-2)2+5的图象的顶点坐标是( )
| A. | (-2,5) | B. | (-2,-5) | C. | (2,-5) | D. | (2,5) |
6.已知关于x的方程x+3a=11与x-4=1的解相同,则a的值是( )
| A. | 5 | B. | -2 | C. | 2 | D. | -5 |
 根据如图所示的程序进行计算,若输入x的值为-3,则输出的值为14.
根据如图所示的程序进行计算,若输入x的值为-3,则输出的值为14.