题目内容
已知:在⊙O中,CD平分∠ACB,弦AB、CD相交于点E,连接AD、BD.(1)写出图中3对相似的三角形(不必证明);
(2)找出图中相等的线段,并说出理由.

【答案】分析:(1)据圆周角定理的推论可以得到有关的角相等,根据两个角对应相等可证明三角形相似;
(2)根据圆周角定理的推论得到等弧,再根据等弧对等弦证明.
解答:解:(1)相似三角形有△AEC∽△DEB、△AED∽△CEB、△ACE∽△BCD等;
(2)AD=BD.理由如下:
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴弧AD=弧BD;
∴AD=BD.
点评:本题要能够熟练运用圆周角定理的推论以及等弧对等弦的性质.
(2)根据圆周角定理的推论得到等弧,再根据等弧对等弦证明.
解答:解:(1)相似三角形有△AEC∽△DEB、△AED∽△CEB、△ACE∽△BCD等;
(2)AD=BD.理由如下:
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴弧AD=弧BD;
∴AD=BD.
点评:本题要能够熟练运用圆周角定理的推论以及等弧对等弦的性质.

练习册系列答案
相关题目
已知,在△ABC中,CD是中线,CD=
AB,那么下列判断错误的是( )
| 1 |
| 2 |
| A、∠DAC=∠DCA |
| B、∠DBC=∠DCB |
| C、∠ACB=90° |
| D、∠A=30° |
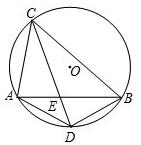 21、已知:在⊙O中,CD平分∠ACB,弦AB、CD相交于点E,连接AD、BD.
21、已知:在⊙O中,CD平分∠ACB,弦AB、CD相交于点E,连接AD、BD.