题目内容
已知平行四边形的高与底边的比是h:a=2:5,用表达式表示平行四边形的面积S与它的底边a的关系,并从图象观察平行四边形的面积随其底边变化而变化的情况.
考点:平行四边形的性质
专题:
分析:首先得出h与a的关系,进而由图象得出平行四边形的面积随其底边变化情况.
解答: 解:∵平行四边形的高与底边的比是h:a=2:5,
解:∵平行四边形的高与底边的比是h:a=2:5,
∴h=
a,
则S=
a×a=
a2,
如图所示:平行四边形的面积随其底边增大而增大.
 解:∵平行四边形的高与底边的比是h:a=2:5,
解:∵平行四边形的高与底边的比是h:a=2:5,∴h=
| 2 |
| 5 |
则S=
| 2 |
| 5 |
| 2 |
| 5 |
如图所示:平行四边形的面积随其底边增大而增大.
点评:此题主要考查了平行四边形的性质以及函数图象性质,利用数形结合得出是解题关键.

练习册系列答案
相关题目
已知一次函数y=(1+2m)x-3中,函数值y随自变量x的增大而增大,那么m的取值范围是( )
A、m>
| ||
B、m<
| ||
C、m<-
| ||
D、m>-
|
已知等腰△ABC的边长为3、5,则腰AC的长可能为( )
| A、5 | B、5或3 | C、3 | D、2 |
下列说法错误的是( )
| A、数轴上的点表示的数,右边的总比左边的数大 | ||
| B、|a|不可能是负数 | ||
C、-
| ||
| D、380000000用科学记数法表示3.8×108 |
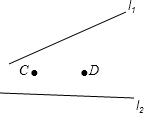 如图,一个人从C点骑马出发到D点,但他必须先到河岸边l1的P1点去让马饮水,然后再到河岸边l2的P2点去,再次让马饮水,最后骑马到D点,他应如何选择饮水点P1,P2.才能使所走的路程CP1+P1P2+P2D最短?
如图,一个人从C点骑马出发到D点,但他必须先到河岸边l1的P1点去让马饮水,然后再到河岸边l2的P2点去,再次让马饮水,最后骑马到D点,他应如何选择饮水点P1,P2.才能使所走的路程CP1+P1P2+P2D最短?