题目内容
11.当x<0时,化简$\sqrt{{x}^{2}-2x+1}$的结果是( )| A. | x-1 | B. | 1-x | C. | (x-1)2 | D. | x+1 |
分析 直接利用二次根式的性质结合完全平方公式化简得出答案.
解答 解:∵x<0,
∴$\sqrt{{x}^{2}-2x+1}$=$\sqrt{(1-x)^{2}}$=1-x.
故选:B.
点评 此题主要考查了二次根式的性质与化简,正确应用二次根式的性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.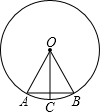 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论中,错误的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论中,错误的是( )
 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论中,错误的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论中,错误的是( )| A. | 弦AB的长等于圆内接正六边形的边长 | |
| B. | $\widehat{AC}$=$\widehat{BC}$ | |
| C. | 弦AC的长等于圆内接正十二边形的边长 | |
| D. | ∠BAC=30° |
16. 已知有理数a、b在数轴上的位置如图,则化简|a-b|+|a+b|的结果为( )
已知有理数a、b在数轴上的位置如图,则化简|a-b|+|a+b|的结果为( )
 已知有理数a、b在数轴上的位置如图,则化简|a-b|+|a+b|的结果为( )
已知有理数a、b在数轴上的位置如图,则化简|a-b|+|a+b|的结果为( )| A. | -2a | B. | 2a | C. | 2b | D. | -2b |
3.已知甲数=2×2×3×5,乙数=2×3×3×5,那么甲数和乙数的最小公倍数是( )
| A. | 60 | B. | 90 | C. | 120 | D. | 180 |
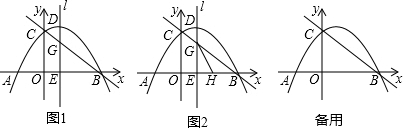
 如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,求证:CA=CD.
如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,求证:CA=CD.

 如图,点B,E,C,F在同一条直线上,AB∥DE,∠A=∠D,试判断∠F与∠ACF的数量关系,并说明理由.
如图,点B,E,C,F在同一条直线上,AB∥DE,∠A=∠D,试判断∠F与∠ACF的数量关系,并说明理由.