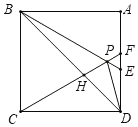
题目内容
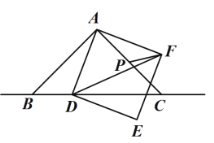
【题目】如图,在![]() 中
中![]() 是直径,点
是直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的切线,与
的切线,与![]() 、
、![]() 的延长线分别交于点
的延长线分别交于点![]() 、
、![]() ,连接
,连接![]() .
.
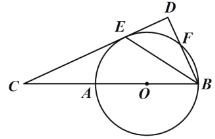
(1)求证:![]() .
.
(2)已知![]() 的半径为2,当
的半径为2,当![]() 为何值时,
为何值时,![]() ,并说明理由.
,并说明理由.
【答案】(1)证明见解析;(2)当![]() 时,
时,![]() .理由见解析.
.理由见解析.
【解析】
(1)连接OE,由点E是![]() 的中点,过点E作⊙O的切线,可得OE⊥CD,BD∥OE,进而得出BD⊥CD;
的中点,过点E作⊙O的切线,可得OE⊥CD,BD∥OE,进而得出BD⊥CD;
(2)当AC=4时,连接AF,证明△AFB∽△BCD,所以![]() ,即BF=DF.
,即BF=DF.
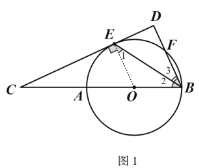
(1)如图1,连接![]() ,
,
∵![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,
,
∴![]() .
.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)当![]() 时,
时,![]() .理由如下:
.理由如下:
如图2,连接![]() ,
,
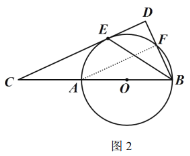
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
由(1)知![]() ,
,
∴![]() ,
,
∴△AFB∽△BCD,
∴![]() ,
,
当![]() 时,
时,
∵![]() 的半径为2,
的半径为2,
∴![]() ,
,
∴BC=AB+AC=8,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目