题目内容
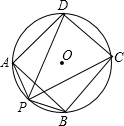如图：圆内接正方形ABCD的边长为| 2 |
| 6 |
| 5 |
分析：连接AC、BD，根据直径对的圆周角是直角得到，∠BPD=∠APC=90°，再利用勾股定理和已知条件求出PC、PD的值．
解答：
解：连接AC、BD，
则AC，BD是圆的直径，且AC=BD=2；
根据直径对的圆周角是直角，∠BPD=∠APC=90°，
由勾股定理得DB2=PB2+PD2，AC2=AP2+PC2，
把PA=1，PB=
，代入解得，
PC=
，PD=
．
解：连接AC、BD，则AC，BD是圆的直径，且AC=BD=2；
根据直径对的圆周角是直角，∠BPD=∠APC=90°，
由勾股定理得DB2=PB2+PD2，AC2=AP2+PC2，
把PA=1，PB=
| 6 |
| 5 |
PC=
| 3 |
| 8 |
| 5 |
点评：本题利用了圆内接的性质，直径对的圆周角是直角，勾股定理求解．
练习册系列答案
相关题目
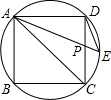如图，在边长为2的圆内接正方形ABCD中，AC是对角线，P为边CD的中点，延长AP交圆于点E．
已知：如图，边长为2的圆内接正方形ABCD中，P为边CD的中点，直线AP交圆于E点．求弦DE的长及△PDE的面积．
如图：圆内接正方形ABCD的边长为
，点P在弧AB上PA=1，PB=
，则PC=________，PD=________．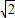
，点P在弧AB上PA=1，PB=
，则PC= ，PD= ．