题目内容
 如图,弓形ABC中,∠BAC=60°,BC=2
如图,弓形ABC中,∠BAC=60°,BC=2| 3 |
0<m<
| 4π |
| 3 |
0<m<
.| 4π |
| 3 |
分析:可设I为△PBC的内心连接BI,利用点I的轨迹是以点D为圆心,2为半径的弧CIB(不含点C、B),可求出弧CIB的长为
,进而求出m的取值范围.
| 4π |
| 3 |
解答:解: 如图,将圆补全,过点O作OD⊥BC交⊙O于点D,设I为△PBC的内心连接BI、连接PD、
如图,将圆补全,过点O作OD⊥BC交⊙O于点D,设I为△PBC的内心连接BI、连接PD、
连接BO、连接CO、连接BD、连接CD、连接PB、连接PC,
∵DO⊥BC,
∴BD=CD,∠BPD=∠CPD,
∵PBI+∠BPI=∠BID,∠DBC+∠CBI=∠IBD,∠BPD=∠BCD,
∴∠DBI=∠BID,
∴ID=BD,
∵∠BAC=60°,BC=2
,
∴∠BOD=60°,△BDO是等边三角形,
∴BO=
=2,
∴BD=BO=ID=2,
∴动点I到定点D的距离为2,即点I的轨迹是以点D为圆心,2为半径的弧CIB(不含点C、B),
弧CIB的长为
,
则m的取值范围是0<m<
.
故答案为:0<m<
.
 如图,将圆补全,过点O作OD⊥BC交⊙O于点D,设I为△PBC的内心连接BI、连接PD、
如图,将圆补全,过点O作OD⊥BC交⊙O于点D,设I为△PBC的内心连接BI、连接PD、连接BO、连接CO、连接BD、连接CD、连接PB、连接PC,
∵DO⊥BC,
∴BD=CD,∠BPD=∠CPD,
∵PBI+∠BPI=∠BID,∠DBC+∠CBI=∠IBD,∠BPD=∠BCD,
∴∠DBI=∠BID,
∴ID=BD,
∵∠BAC=60°,BC=2
| 3 |
∴∠BOD=60°,△BDO是等边三角形,
∴BO=
| ||
| sin60° |
∴BD=BO=ID=2,
∴动点I到定点D的距离为2,即点I的轨迹是以点D为圆心,2为半径的弧CIB(不含点C、B),
弧CIB的长为
| 4π |
| 3 |
则m的取值范围是0<m<
| 4π |
| 3 |
故答案为:0<m<
| 4π |
| 3 |
点评:此题主要考查了圆心角、圆周角定理以及三角形内心的性质等知识,本题需仔细分析题意,结合图形,得出I的运动路径即可解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 以点P为圆心,PA为半径画⊙P交AC于点Q.
以点P为圆心,PA为半径画⊙P交AC于点Q.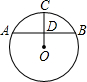 如图,已知⊙O中弦AB=2,弓形高CD=2-
如图,已知⊙O中弦AB=2,弓形高CD=2- 如图,弓形ABC中,∠BAC=60°,BC=2
如图,弓形ABC中,∠BAC=60°,BC=2 ,若点P在优弧BAC上由点B向点C移动,记△PBC的内心为I,点I随点P的移动所经过的路程为m,则m的取值范围为________.
,若点P在优弧BAC上由点B向点C移动,记△PBC的内心为I,点I随点P的移动所经过的路程为m,则m的取值范围为________.