Question

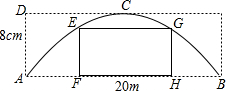有一个抛物线形拱桥，其最大高度AD为8m，跨度AB为20m，为了对拱桥进行加固，需要在拱桥内安装矩形脚手架EFHG，已知脚手架的高EF为5m．
（1）请建立合适直角坐标系，并求抛物线的解析式；
（2）求出矩形脚手架EG的长．（参考数据：

6

≈2.45，计算结果精确到0.1m）

Answer 1

考点：二次函数的应用

专题：压轴题

分析：（1）以抛物线的顶点C为坐标原点，以水平方向为x轴建立平面直角坐标系，就可以表示出C点的坐标，B点的坐标由待定系数法就可以求出其解析式；
（2）由四边形EFHG是矩形就可以得出EF=GH=5，就可以求出E、G的纵坐标，将其纵坐标代入函数的解析式求出其解就可以求出点的坐标，而得出结论．

解答：解：（1）以抛物线的顶点C为坐标原点，以水平方向为x轴建立平面直角坐标系，
则C（0，0），B（10，-8），
设抛物线的解析式为y=ax²，由题意，得
-8=100a，
解得a=-

2

25

，
故抛物线的解析式为：y=-

2

25

x²；

（2）∵四边形EFHG是矩形，
∴EF=GH=5，
∴E、G的纵坐标为-3，
∴-3=-

2

25

x²，
x=±

5 6

2

，
∴E（-

5 6

2

，-3），G（

5 6

2

，-3），
∴EG=

5 6

2

-（-

5 6

2

）=5

6

．
∵

6

≈2.45，
∴EG=5×2.45=12.3（m）．

点评：本题是一道二次函数的综合试题，考查了待定系数法求二次函数的解析式的运用，矩形的性质的运用，由自变量的值求函数的值的运用，解答时求出函数的解析式是关键．