题目内容
 如图,正六边形ABCDEF为⊙0的内接正六边形,连结AE.已知⊙0的半径为2cm.
如图,正六边形ABCDEF为⊙0的内接正六边形,连结AE.已知⊙0的半径为2cm.(1)求∠AED的度数和弧AB的长.
(2)求正六边形ABCDEF与⊙O的面积之比.
考点:正多边形和圆
专题:
分析:(1)根据六边形的内角和求出∠F的度数,从而得出∠AEF的度数,进而得出∠AED的度数,连接OA、OB,求出圆心角∠AOB的度数,再利用弧长公式解答即可;
(2)求得三角形AOB的面积,再乘以6即可得出正六边形ABCDEF的面积,再求出圆的面积,求出面积之比即可.
(2)求得三角形AOB的面积,再乘以6即可得出正六边形ABCDEF的面积,再求出圆的面积,求出面积之比即可.
解答: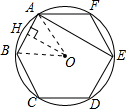 解:(1)∵ABCDEF为正六边形,
解:(1)∵ABCDEF为正六边形,
∴∠F=120°,∠AEF=30°,
∴∠AED=120°-30°=90°,
∴∠AOB=360°×
=60°,
弧AB的长为
=
πcm.
(2)过点O作OH⊥AB垂足为H,
∵∠AOH=30°,OA=2cm,
∴由勾股定理得OH=
cm,
S△AOB=
AB•OH=
×2×
=
cm2,
∴正六边形ABCDEF的面积=6×S△AOB=6
cm2,
⊙O的面积=π22=4πcm2,
∴正六边形ABCDEF与⊙O的面积之比=6
:4π=3
:2π.
 解:(1)∵ABCDEF为正六边形,
解:(1)∵ABCDEF为正六边形,∴∠F=120°,∠AEF=30°,
∴∠AED=120°-30°=90°,
∴∠AOB=360°×
| 1 |
| 6 |
弧AB的长为
| 60•π•2 |
| 180 |
| 2 |
| 3 |
(2)过点O作OH⊥AB垂足为H,
∵∠AOH=30°,OA=2cm,
∴由勾股定理得OH=
| 3 |
S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴正六边形ABCDEF的面积=6×S△AOB=6
| 3 |
⊙O的面积=π22=4πcm2,
∴正六边形ABCDEF与⊙O的面积之比=6
| 3 |
| 3 |
点评:本题考查了正多边形和圆,将扇形的弧长公式与多边形的性质相结合,构思巧妙,利用了正六边形的性质,是一道好题.此题综合性较强,难度不大,解题的关键是注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
在△ABC中,已知∠A=40°,∠B=50°,则此三角形是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法判断 |
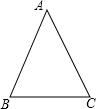 如图,已知在△ABC中,AB=AC=13,BC=10,求∠A、∠B的正弦值.
如图,已知在△ABC中,AB=AC=13,BC=10,求∠A、∠B的正弦值.