题目内容
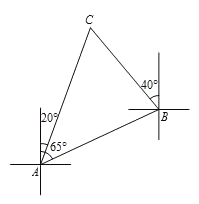
【题目】如图,一艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:(1)∠C的度数;
(2)A,C两港之间的距离为多少km.
【答案】(1)∠C=60°(2)AC=![]()
【解析】
(1)根据方位角的概念确定∠ACB=40°+20°=60;
(2)AB=30![]() ,过B作BE⊥AC于E,解直角三角形即可得到结论.
,过B作BE⊥AC于E,解直角三角形即可得到结论.
解:(1)如图,在点C处建立方向标
根据题意得,AF∥CM∥BD
∴∠ACM=∠FAC, ∠BCM=∠DBC
∴∠ACB=∠ACM+∠BCM=40°+20°=60°,
(2)∵AB=30![]() ,过B作BE⊥AC于E,
,过B作BE⊥AC于E,
∴∠AEB=∠CEB=90°,
在Rt△ABE中,∵∠ABE=45°,AB=30![]() ,
,
∴AE=BE=![]() AB=30km,
AB=30km,
在Rt△CBE中,∵∠ACB=60°,
∴CE=![]() BE=10
BE=10![]() km,
km,
∴AC=AE+CE=30+10![]() ,
,
∴A,C两港之间的距离为(30+10![]() )km,
)km,


练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目