题目内容
19.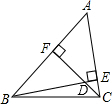 如图,已知BE和CF是△ABC的两条高,∠ABC=48°,∠ACB=76°,则∠FDE=124°.
如图,已知BE和CF是△ABC的两条高,∠ABC=48°,∠ACB=76°,则∠FDE=124°.
分析 由三角形的内角和定理求出∠A的度数,再有四边形AFDE的内角和求出∠FDE的度数.
解答 解:(法一)在△ABC中,
∵∠A+∠ABC+∠ACB=180°
∴∠A=180°-48°-76°=56°
在四边形AFDE中,
∵∠A+∠AFC+∠AEB+∠FDE=360°
又∵∠AFC=∠AEB=90°,∠A=56°
∴∠FDE=360°-90°-90°-56°
=124°
故答案为:124°
(法二)∵∠AEB=∠ACB+∠EBC=90°,∠AFC=∠ABC+∠FCB=90°,
∴∠CBE=14°,∠FCB=42°,
∵∠BDC=180°-∠CBE-∠FCB=124°,
∴∠FDE=124°.
故答案为:124°
点评 本题考查了三角形的内角和定理和四边形的内角和.三角形的内角和是180°,四边形的内角和是360°,n边形的内角和为(n-2)•180°(n为正整数,n≥3).

练习册系列答案
相关题目
9.某体育场计划修建一个容积一定的长方体游泳池,若容积为V(m3),游泳池的底面积S(m2)与其深度d(m)之间的函数关系式为S=$\frac{V}{d}$(d>0),则该函数的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
7. 如图,a,b是数轴上的两个有理数,下面说法中正确的是( )
如图,a,b是数轴上的两个有理数,下面说法中正确的是( )
 如图,a,b是数轴上的两个有理数,下面说法中正确的是( )
如图,a,b是数轴上的两个有理数,下面说法中正确的是( )| A. | a>b | B. | b>a | C. | $\frac{a}{b}>0$ | D. | a+b<0 |
11.下面每组数分别是三根小木棒的长度(单位:cm),用它们能摆成三角形的是( )
| A. | 3,4,8 | B. | 12,13,5 | C. | 7,8,15 | D. | 1,6,3 |
9.要使分式$\frac{2}{x+1}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x<1 | D. | x≠-1 |
 如图,若△ADE∽△ACB,AB=8,AE=4,DE=3,则BC=6.
如图,若△ADE∽△ACB,AB=8,AE=4,DE=3,则BC=6.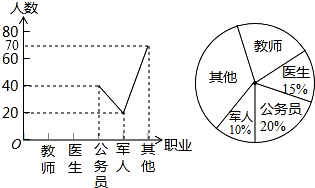 某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,并根据这组数据绘制下面两幅不完整的统计图:
某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,并根据这组数据绘制下面两幅不完整的统计图: 已知:如图,AB比AC长2cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,求AB和AC的长.
已知:如图,AB比AC长2cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,求AB和AC的长.