题目内容
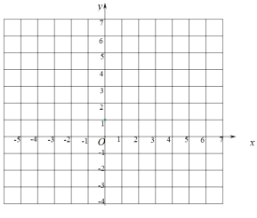
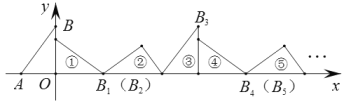
【题目】如图,在平面直角坐标系中,已知点A(-1.5,0),B(0,2),将△ABO顺着x轴的正半轴无滑动的滚动,第一次滚动到①的位置,点B的对应点记作B1;第二次滚动到②的位置,点B1的对应点记作B2;第三次滚动到③的位置,点B2的对应点记作B3;![]() ;依次进行下去,则点B2020的坐标为__________.
;依次进行下去,则点B2020的坐标为__________.
【答案】![]()
【解析】
先利用翻转的性质、点坐标的变化规律分别求出点![]() 的坐标,再归纳总结出一般规律,由此即可得出答案.
的坐标,再归纳总结出一般规律,由此即可得出答案.
![]()
![]()
由翻转的性质得:![]() ,则
,则![]()
由翻转过程可知,点![]() 重合,则
重合,则![]()
点![]() 的横坐标为
的横坐标为![]() ,纵坐标为2,即
,纵坐标为2,即![]()
同理可得:点![]() 重合,点
重合,点![]() 的横坐标为
的横坐标为![]() ,纵坐标为0
,纵坐标为0
即![]() ,
,![]()
点![]() 的横坐标为
的横坐标为![]() ,纵坐标为2,即
,纵坐标为2,即![]()
归纳类推得出以下规律:(其中,n为正整数)
(1)点![]() 的横坐标变化规律为
的横坐标变化规律为![]() ,纵坐标均为0
,纵坐标均为0
(2)点![]() 的横坐标变化规律为
的横坐标变化规律为![]() ,纵坐标均为0
,纵坐标均为0
(3)点![]() 的横坐标变化规律为
的横坐标变化规律为![]() ,纵坐标均为2
,纵坐标均为2
![]()
![]() 点
点![]() 的坐标变化规律符合(1)
的坐标变化规律符合(1)
则点![]() 的横坐标为
的横坐标为![]() ,纵坐标为0,即
,纵坐标为0,即![]()
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目