题目内容
12.已知关于x的一元二次方程x2-2x+m=0有两个不相等的实数根,则m的取值范围是( )| A. | m>1 | B. | m>-1 | C. | m<-1 | D. | m<1 |
分析 根据判别式的意义得到△=(-2)2-4m>0,然后解不等式即可.
解答 解:根据题意得△=(-2)2-4m>0,
解得m<1.
故选D.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
2.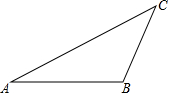 如图,已知:△ABC,请按下列要求用尺规作图(保留痕迹,不写作法及证明):
如图,已知:△ABC,请按下列要求用尺规作图(保留痕迹,不写作法及证明):
(1)作AB边的垂直平分线l,垂足为点D;
(2)在(1)中所得直线l上,求作一点M,使点M到BC边所在直线的距离等于MD.
 如图,已知:△ABC,请按下列要求用尺规作图(保留痕迹,不写作法及证明):
如图,已知:△ABC,请按下列要求用尺规作图(保留痕迹,不写作法及证明):(1)作AB边的垂直平分线l,垂足为点D;
(2)在(1)中所得直线l上,求作一点M,使点M到BC边所在直线的距离等于MD.
2.式子(11+6$\sqrt{2}$)的算术平方根是( )
| A. | 3-$\sqrt{2}$ | B. | 3+$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | -3-$\sqrt{2}$ |
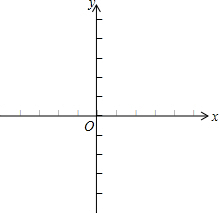 使用五点法画出二次函数y=x2-2x-3的图象.
使用五点法画出二次函数y=x2-2x-3的图象.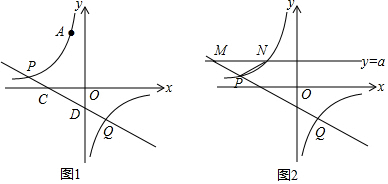
 如图,AB=DE,BC=EF,CD=FA,∠A=∠D,求证:∠ABC=∠DEF.
如图,AB=DE,BC=EF,CD=FA,∠A=∠D,求证:∠ABC=∠DEF.