题目内容
20. 如图,在△ABC中,AC=6,BC=9,D是△ABC的边BC上的点,且∠CAD=∠B,那么CD的长是4.
如图,在△ABC中,AC=6,BC=9,D是△ABC的边BC上的点,且∠CAD=∠B,那么CD的长是4.
分析 由∠C=∠C,∠CAD=∠B,根据有两角对应相等的三角形相似,可得△ACD∽△BCA,又由相似三角形的对应边成比例,易求得CD的长.
解答 解:∵∠C=∠C,∠CAD=∠B,
∴△ACD∽△BCA,
∴$\frac{AC}{BC}$=$\frac{CD}{AC}$,
即$\frac{6}{9}$=$\frac{CD}{6}$,
∴CD的长是4.
故答案为:4.
点评 此题考查了相似三角形的判定与性质.注意有两角对应相等的三角形相似,相似三角形的对应边成比例.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
9.某射击运动员在相同条件下的射击160次,其成绩记录如下:
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率0.8(精确到0.1).
| 射击次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
| 射中9环以上的次数 | 15 | 33 | 48 | 63 | 79 | 97 | 111 | 130 |
| 射中9环以上的频率 | 0.75 | 0.83 | 0.80 | 0.79 | 0.79 | 0.81 | 0.79 | 0.81 |
10.下面图形中,对称轴最多的是( )
| A. | 等边三角形 | B. | 正方形 | C. | 半圆 | D. | 等腰梯形 |
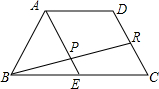 如图,AD∥BC,BC=2AD,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=$\frac{1}{3}$.
如图,AD∥BC,BC=2AD,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=$\frac{1}{3}$.