题目内容
已知二次函数y=-3(x-1)2,下列说法正确的有( )
①因为a=-3,所以开口方向向上;
②顶点坐标为(1,0);
③对称轴为x=1;
④把y=-3x2的图象向右平移1个单位就得y=-3(x-1)2的图象.
①因为a=-3,所以开口方向向上;
②顶点坐标为(1,0);
③对称轴为x=1;
④把y=-3x2的图象向右平移1个单位就得y=-3(x-1)2的图象.
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:二次函数的性质
专题:
分析:根据二次函数的性质对①②③进行判断;
根据二次函数图象与几何变换对④进行判断.
根据二次函数图象与几何变换对④进行判断.
解答:解:对于二次函数y=-3(x-1)2,因为a=-3,所以开口方向向下,所以①错误;
顶点坐标为(1,0),所以②正确;
对称轴为直线x=1,所以③错误;
y=-3x2的图象向右平移1个单位就得y=-3(x-1)2的图象,所以④正确.
故选B.
顶点坐标为(1,0),所以②正确;
对称轴为直线x=1,所以③错误;
y=-3x2的图象向右平移1个单位就得y=-3(x-1)2的图象,所以④正确.
故选B.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值4ac-b24a,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值4ac-b24a,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
以下五家银行行标中,是轴对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
若点P关于x轴的对称点的坐标是(2,3),则点P关于原点的对称点的坐标是( )
| A、(-3,-2) |
| B、(2,-3) |
| C、(-2,-3) |
| D、(-2,3) |
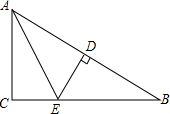 如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于( )
如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于( )| A、1cm | B、2cm |
| C、3cm | D、4cm |
 如图,AD为等边三角形的高,DE是△ADC的高,已知△ABC的边长为6,求AE的长.
如图,AD为等边三角形的高,DE是△ADC的高,已知△ABC的边长为6,求AE的长.