题目内容
你会求(a-1)(a2012+a2011+a2010+‥‥a2+a+1)的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
(a-1)(a+1)=a2-1
(a-1)(a2+a+1)=a3-1;
(a-1)(a3+a2+a+1)=a4-1;
(1)由上面的规律我们可以大胆猜想,得到(a-1)(a2012+a2011+a2010+‥‥a2+a+1)=
利用上面的结论,求
(2)22013+22012+22011+‥‥22+2+1的值是
(3)求52013+52012+52011+‥‥52+5+1的值.
(a-1)(a+1)=a2-1
(a-1)(a2+a+1)=a3-1;
(a-1)(a3+a2+a+1)=a4-1;
(1)由上面的规律我们可以大胆猜想,得到(a-1)(a2012+a2011+a2010+‥‥a2+a+1)=
a2013-1
a2013-1
.利用上面的结论,求
(2)22013+22012+22011+‥‥22+2+1的值是
22014-1
22014-1
. (3)求52013+52012+52011+‥‥52+5+1的值.
分析:(1)根据题意得到(a-1)(a2012+a2011+a2010+‥‥a2+a+1)=a2013-1;
(2)将得出的规律中的a换为2,计算即可得到结果;
(3)将a换为5,计算即可得到结果.
(2)将得出的规律中的a换为2,计算即可得到结果;
(3)将a换为5,计算即可得到结果.
解答:解:(1)由上面的规律我们可以大胆猜想,得到(a-1)(a2012+a2011+a2010+‥‥a2+a+1)=a2013-1;
(2)∵(2-1)(22013+22012+22011+‥‥22+2+1)=22014-1,
∴22013+22012+22011+‥‥22+2+1的值是22014-1;
(3)∵(5-1)(52013+52012+52011+‥‥52+5+1)=52014-1,
∴52013+52012+52011+‥‥52+5+1=
(52014-1).
故答案为:(1)a2013-1;(2)22014-1
(2)∵(2-1)(22013+22012+22011+‥‥22+2+1)=22014-1,
∴22013+22012+22011+‥‥22+2+1的值是22014-1;
(3)∵(5-1)(52013+52012+52011+‥‥52+5+1)=52014-1,
∴52013+52012+52011+‥‥52+5+1=
| 1 |
| 4 |
故答案为:(1)a2013-1;(2)22014-1
点评:此题考查了整式的混合运算,弄清题中的规律是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
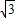 的整数部分吗?阅读后再解答.
的整数部分吗?阅读后再解答.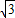 <2,
<2,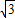 >-2,
>-2,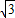 >4-2,
>4-2,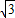 >2.
>2.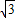 =2+b.整数部分为______,小数部分b=______
=2+b.整数部分为______,小数部分b=______