Question

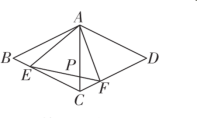
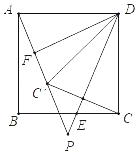
【题目】如图，在平行四边形ABCD中，E是边AD上一点，CE与BD相交于点O，CE与BA的延长线相交于点G，已知DE＝2AE，CE＝8．

（1）求GE的长；

（2）若＝，＝，用、表示;

（3）在图中画出+．（不需要写画法，但需要结论）

Answer 1

【答案】（1）GE＝4；（2）；（3）即为所求

【解析】

（1）利用平行线分线段成比例定理解决问题即可．

（2）利用三角形法则即可求出，再利用平行线分线段成比例定理即可解决问题．

（3）如图，延长CD到H，使得DH＝AG，连接AH．则即为所求．

解：（1）∵四边形AB平行四边形，

∴AD＝BC，AD∥BC，

∵DE＝2AE，

∴＝＝，

∵CE＝8，

∴＝，

∴GE＝4．

（2）∵＝+＝﹣，DE∥BC，DE＝2AE，

∴＝＝，

∴＝，

∴＝﹣（﹣）＝﹣

（3）如图，延长CD到H，使得DH＝AG，连接AH．则即为所求．

∵AE∥BC，

∴＝＝，

∴＝，

∴＝＝＝

∴＝＝，

∴即为所求．