题目内容
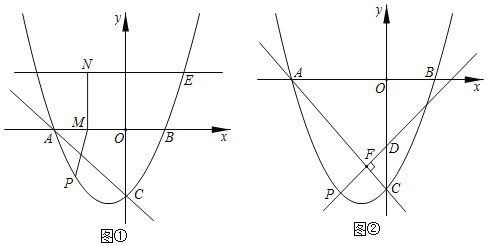
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,抛物线上的点
,抛物线上的点![]() 的横坐标为3,过点
的横坐标为3,过点![]() 作直线
作直线![]() 轴.
轴.
(1)点![]() 为抛物线上的动点,且在直线
为抛物线上的动点,且在直线![]() 的下方,点
的下方,点![]() ,
,![]() 分别为
分别为![]() 轴,直线
轴,直线![]() 上的动点,且
上的动点,且![]() 轴,当
轴,当![]() 面积最大时,求
面积最大时,求![]() 的最小值;
的最小值;
(2)过(1)中的点![]() 作
作![]() ,垂足为
,垂足为![]() ,且直线
,且直线![]() 与
与![]() 轴交于点
轴交于点![]() ,把
,把![]() 绕顶点
绕顶点![]() 旋转45°,得到
旋转45°,得到![]() ,再把
,再把![]() 沿直线
沿直线![]() 平移至
平移至![]() ,在平面上是否存在点
,在平面上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在直接写出点
为顶点的四边形为菱形?若存在直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() (2)
(2)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)根据题意求得点![]() 、
、![]() 、
、![]() 、
、![]() 的坐标,进而求得直线
的坐标,进而求得直线![]() 和直线
和直线![]() 解析式.过点
解析式.过点![]() 作
作![]() 轴垂线
轴垂线![]() 交
交![]() 于点
于点![]() ,设点
,设点![]() 横坐标为
横坐标为![]() ,即能用
,即能用![]() 表示
表示![]() 、
、![]() 的坐标进而表示
的坐标进而表示![]() 的长.由
的长.由![]() 得到关于
得到关于![]() 的二次函数,即求得
的二次函数,即求得![]() 为何值时
为何值时![]() 面积最大,求得此时点
面积最大,求得此时点![]() 坐标.把点
坐标.把点![]() 向上平移
向上平移![]() 的长,易证四边形
的长,易证四边形![]() 是平行四边形,故有
是平行四边形,故有![]() .在直线
.在直线![]() 的上方以
的上方以![]() 为斜边作等腰
为斜边作等腰![]() ,则有
,则有![]() .所以
.所以![]() ,其中
,其中![]() 的长为定值,易得当点
的长为定值,易得当点![]() 、
、![]() 、
、![]() 在同一直线上时,线段和的值最小.又点
在同一直线上时,线段和的值最小.又点![]() 是动点,
是动点,![]() ,由垂线段最短可知过点
,由垂线段最短可知过点![]() 作
作![]() 的垂线段
的垂线段![]() 时,
时,![]() 最短.求直线
最短.求直线![]() 、
、![]() 解析式,联立方程组即求得点
解析式,联立方程组即求得点![]() 坐标,进而求得
坐标,进而求得![]() 的长.
的长.
(2)先求得![]() ,
,![]() ,
,![]() 的坐标,可得
的坐标,可得![]() 是等腰直角三角形,当
是等腰直角三角形,当![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 再沿直线
再沿直线![]() 平移可得△
平移可得△![]() ,根据以
,根据以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形,可得
为顶点的四边形为菱形,可得![]() ,
,![]() ,
,![]() ,
,![]() ,即可求得
,即可求得![]() 的坐标,当
的坐标,当![]() 绕
绕![]() 顺时针旋转
顺时针旋转![]() 再沿直线
再沿直线![]() 平移可得△
平移可得△![]() ,根据以
,根据以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形,可得
为顶点的四边形为菱形,可得![]() ,
,![]() ,即可求得
,即可求得![]() 的坐标.
的坐标.
解:(1)如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,

以![]() 为斜边在直线
为斜边在直线![]() 上方作等腰
上方作等腰![]() ,过点
,过点![]() 作
作![]() 于点
于点![]()
![]() 时,
时,![]()
![]()
![]() 时,
时,![]()
解得:![]() ,
,![]()
![]() ,
,![]()
![]() 直线
直线![]() 解析式为
解析式为![]()
![]() 抛物线上的点
抛物线上的点![]() 的横坐标为3
的横坐标为3
![]()
![]() ,直线
,直线![]()
![]() 点
点![]() 在
在![]() 轴上,点
轴上,点![]() 在直线
在直线![]() 上,
上,![]() 轴
轴
![]()
设抛物线上的点![]() ,
,![]()
![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() 最大
最大
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]() 等腰
等腰![]() 中,
中,![]() 为斜边
为斜边
![]() ,
,![]()
![]()
![]()
![]() 当点
当点![]() 、
、![]() 、
、![]() 在同一直线上时,
在同一直线上时,![]() 最小
最小
![]()
设直线![]() 解析式为
解析式为![]()
![]() 解得:
解得:![]()
![]() 直线
直线![]()
设直线![]() 解析式为
解析式为![]()
![]() 解得:
解得:![]()
![]() 直线
直线![]()
![]()
 解得:
解得:![]()
![]() ,
,![]()
![]()
![]() 最小值为
最小值为![]()
(2)![]() ,
,![]() ,
,
![]() 直线
直线![]() 解析式为:
解析式为:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
如图2,把![]() 绕顶点
绕顶点![]() 逆时针旋转
逆时针旋转![]() ,得到△
,得到△![]() ,
,![]() ,
,![]() ,
,![]()
把△![]() 沿直线
沿直线![]() 平移至△
平移至△![]() ,连接
,连接![]() ,
,![]()

则直线![]() 解析式为
解析式为![]() ,直线
,直线![]() 解析式为
解析式为![]() ,显然
,显然![]()
![]() 以
以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形,
为顶点的四边形为菱形,![]() 不可能为边,只能以
不可能为边,只能以![]() 、
、![]() 为邻边构成菱形
为邻边构成菱形
![]() ,
,
![]() ,
,![]()
![]()
![]() ,
,![]() ,
,
如图3,把![]() 绕顶点
绕顶点![]() 顺时针旋转
顺时针旋转![]()

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案