Question

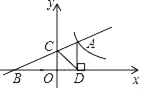
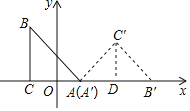
【题目】如图，等腰直角三角形ABC在平面直角坐标系中，直角边AC在x轴上，O为AC的中点，点A的坐标为（1，0），将△ABC绕点A顺时针旋转135°，使斜边AB的对应边A′B′与x轴重合，则点C的对应点C'的坐标为（　　）

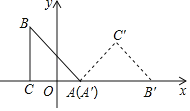
A. （2，2）B. （1+ ，）C. （1+，2）D. （2，2+）

Answer 1

【答案】B

【解析】

根据已知条件得到AC＝2，根据勾股定理得到AB＝2，由旋转的性质得到A′B′＝AB＝2，过C′作C′D⊥x轴于D，根据等腰直角三角形的性质即可得到结论．

解：∵O为AC的中点，点A的坐标为（1，0），

∴AC＝2，

∵△ABC是等腰直角三角形，

∴AB＝2，

∵将△ABC绕点A顺时针旋转135°，使斜边AB的对应边A′B′与x轴重合，

∴A′B′＝AB＝2，

过C′作C′D⊥x轴于D，

∴C′D＝A′D＝A′B′＝，

∴OD＝1+，

∴点C的对应点C'的坐标为（1+，），

故选：B．