题目内容
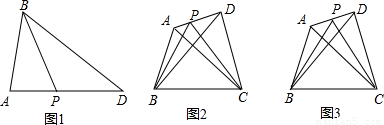
点P是△ABD中AD边上一点，
【小题1】如图1，当P为AD中点时，则有S△ABP= S△ABD；
【小题2】如图2，在四边形ABCD中，P是AD边上任意一点，△PBC的面积为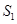
，△ABC的面积为
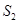，△DBC的面积为
。
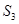①当AP=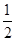
AD时，如图3，试探究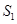、、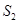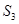之间的关系？写出求解过程；
②一般地，当AP=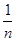
AD（n表示正整数）时，试探究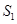、、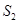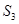之间的关系？写出求解过程。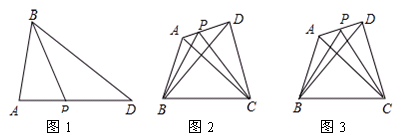
【小题1】S△ABP=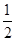S△ABD；
【小题2】①当AP=
AD时（如图②）：
∵AP=AD，△ABP和△ABD的高相等，
∴S△ABP=S△ABD。
∵PD=AD－AP=
AD，△CDP和△CDA的高相等，
∴S△CDP=S△CDA。
∴S△PBC=S四边形ABCD－S△ABP－S△CDP
=S四边形ABCD－S△ABD－S△CDA
=S四边形ABCD－（S四边形ABCD－S△DBC）－（S四边形ABCD－S△ABC）
=S△DBC＋S△ABC。
②S△PBC=
S△DBC＋
S△ABC；
∵AP=AD，△ABP和△ABD的高相等，
∴S△ABP=S△ABD。
又∵PD=AD－AP=AD，△CDP和△CDA的高相等，
∴S△CDP=S△CDA
∴S△PBC=S四边形ABCD－S△ABP－S△CDP
=S四边形ABCD－S△ABD－S△CDA
=S四边形ABCD－（S四边形ABCD－S△DBC）－（S四边形ABCD－S△ABC）
=
S△DBC＋
S△ABC。
∴S△PBC=S△DBC＋S△ABC
解析
练习册系列答案
阅读快车系列答案
相关题目
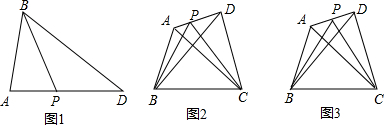
如图，在△ABC中，∠C是直角，AD平分∠BAC交BC于点D．如果AB=8，CD=2那么△ABD的面积等于
，△ABC的面积为
，△DBC的面积为
。
AD时，如图3，试探究
AD（n表示正整数）时，试探究
S△BDP，如图2，在四边形ABCD中，P是AD边上任意一点，探究：
AD时，如图3，△PBC与△ABC和△DBC的面积之间有什么关系？写出求解过程；
AD时，探究S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；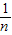
AD（n表示正整数）时，探究S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；
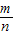AD（0≤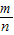
≤1）时，直接写出S△PBC与S△ABC和S△DBC之间的关系．