题目内容
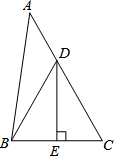
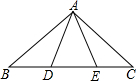
已知等腰三角形ABC的顶角A为120°，底边长为20cm，求腰长．
作AD⊥BC于D．
∵∠BAC=120°，AB=AC，
∴底边上的高AD，即中线AD，∠B=
（180°-120°）=30°．
∵底边长为20cm，
∴BD=10cm，
∴AD=
AB．（直角三角形中30°所对直角边等于斜边的一半），
∴AB2-（
AB）2=102，
解得AB=
．
答：腰长为
．
∵∠BAC=120°，AB=AC，
∴底边上的高AD，即中线AD，∠B=
| 1 |
| 2 |
∵底边长为20cm，
∴BD=10cm，
∴AD=
| 1 |
| 2 |
∴AB2-（
| 1 |
| 2 |
解得AB=
20
| ||
| 3 |
答：腰长为
20
| ||
| 3 |
练习册系列答案
相关题目
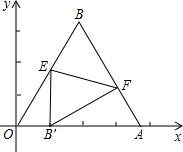正方向上，将△OAB折叠，使点B落在边OA上，记为B′，折痕为EF．