题目内容
设a,b,c是从1到9的互不相同的整数,求 的最大的可能值.
的最大的可能值.
解:设p= ,在上式中,让a,b暂时不变,只让c变,c可取1到9中的各整数,
,在上式中,让a,b暂时不变,只让c变,c可取1到9中的各整数,
则由p= =
= 知,
知,
当c=1时,p取最大值,故c=1.
于是,p= =
= ,在此式中,让a暂时不变,只让b变,b可取2到9中的各整数,
,在此式中,让a暂时不变,只让b变,b可取2到9中的各整数,
则由上式知,当b=2时,p取得最大值,故b=2.
此时,p= +
+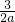 .∴当a取最小值时,p取最大值,而a取3到9中的各整数,所以a=3.
.∴当a取最小值时,p取最大值,而a取3到9中的各整数,所以a=3.
故当a=3,b=2,c=1(字母可互换)时,p取最大值1.
故最大可能值是1.
分析:设p= ,令a,b暂时不变求出c的值,然后再令a不变,求出b的值,从而即可求出答案.
,令a,b暂时不变求出c的值,然后再令a不变,求出b的值,从而即可求出答案.
点评:本题考查了分式的化简求值,难度适中,关键是令a,b暂时不变求出c的值,然后再令a不变,求出b的值,进而求解.
 ,在上式中,让a,b暂时不变,只让c变,c可取1到9中的各整数,
,在上式中,让a,b暂时不变,只让c变,c可取1到9中的各整数,则由p=
 =
= 知,
知,当c=1时,p取最大值,故c=1.
于是,p=
 =
= ,在此式中,让a暂时不变,只让b变,b可取2到9中的各整数,
,在此式中,让a暂时不变,只让b变,b可取2到9中的各整数,则由上式知,当b=2时,p取得最大值,故b=2.
此时,p=
 +
+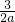 .∴当a取最小值时,p取最大值,而a取3到9中的各整数,所以a=3.
.∴当a取最小值时,p取最大值,而a取3到9中的各整数,所以a=3.故当a=3,b=2,c=1(字母可互换)时,p取最大值1.
故最大可能值是1.
分析:设p=
 ,令a,b暂时不变求出c的值,然后再令a不变,求出b的值,从而即可求出答案.
,令a,b暂时不变求出c的值,然后再令a不变,求出b的值,从而即可求出答案.点评:本题考查了分式的化简求值,难度适中,关键是令a,b暂时不变求出c的值,然后再令a不变,求出b的值,进而求解.

练习册系列答案
相关题目