Question

如图，两个观察者从A，B两地观测空中C处一个气球，分别测得仰角为45º和60º．已知A，B两地相距30米，延长AB，作CD⊥AD于D，当气球沿着与AB平行的方向飘移到点时，在A处又测得气球的仰角为30º，求CD与的长度．（结果保留根号）

Answer 1

CD=（45＋15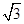）米，CC’=30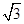米

解析试题分析：
（1）过点C′作AD的延长线的垂线，垂足为D′
在R t △ACD中，∵∠CAD＝45º，则CD＝AD＝x
在R t △BCD中，∠ CBD＝60º，则BD＝x
∵AD－BD="AB," 即 x－x＝30，
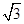∴求得x＝CD＝（米）＝（45＋15）（米）
在R t △AC’D’中，，∴＝45＋45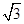
∴CC′=AD′－CD＝30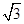
考点：三角函数的应用
点评：该题是常考题，主要考查学生对三角函数的理解和应用，在直角三角形中，涉及到特殊角和边的长度，就要考虑到三角函数值。