题目内容
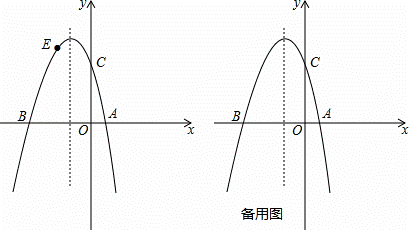
如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),
∴OB=3,
∵OC=OB,
∴OC=3,
∴c=3,
∴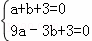 ,
,
解得: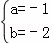 ,
,
∴所求抛物线解析式为:y=﹣x2﹣2x+3;
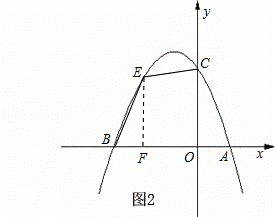
(2)如图2,过点E作EF⊥x轴于点F,设E(a,﹣a2﹣2a+3)(﹣3<a<0)
∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,
∴S四边形BOCE=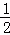 BF•EF+
BF•EF+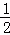 (OC+EF)•OF,
(OC+EF)•OF,
=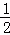 (a+3)•(﹣a2﹣2a+3)+
(a+3)•(﹣a2﹣2a+3)+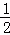 (﹣a2﹣2a+6)•(﹣a),
(﹣a2﹣2a+6)•(﹣a),
=﹣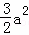 ﹣
﹣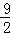 a+
a+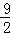 ,
,
=﹣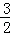 (a+
(a+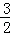 )2+
)2+ ,
,
∴当a=﹣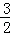 时,S四边形BOCE最大,且最大值为
时,S四边形BOCE最大,且最大值为 .
.
此时,点E坐标为(﹣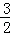 ,
,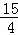 );
);
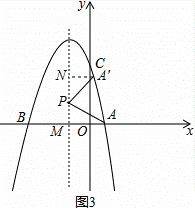
(3)∵抛物线y=﹣x2﹣2x+3的对称轴为x=﹣1,点P在抛物线的对称轴上,
∴设P(﹣1,m),
∵线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,如图,
∴PA=PA′,∠APA′=90°,
如图3,过A′作A′N⊥对称轴于N,设对称轴于x轴交于点M,
∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°,
∴∠NA′P=∠NPA,
在△A′NP与△APM中,
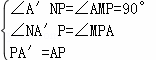 ,
,
∴△A′NP≌△PMA,
∴A′N=PM=|m|,PN=AM=2,
∴A′(m﹣1,m+2),
代入y=﹣x2﹣2x+3得:m +2=﹣(m﹣1)2﹣2(m﹣1)+3,
+2=﹣(m﹣1)2﹣2(m﹣1)+3,
解得:m=1,m=﹣2,
∴P(﹣1,1),(﹣1,﹣2).

 的自变量x的取值范围是____________.
的自变量x的取值范围是____________. 相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C.
 ,则y的最小值为( )
,则y的最小值为( )

 ,则AB:DE= .
,则AB:DE= .